题目内容
9.如图,已知∠1=60°,∠C+∠D+∠E+∠F+∠A+∠B=240°.
分析 由三角形的外角性质和三角形内角和定理即可得出结果.
解答 解:如图所示:
由三角形的外角性质得:∠BMH=∠A+∠C,∠BHM=∠F+∠BGF=∠F+∠1,
∵∠BMH+∠BHM+∠B=180°,∠1+∠D+∠F=180°,
∴∠C+∠D+∠E+∠F+∠A+∠B
=∠BMH+∠BHM+∠B+∠1+∠D+∠E-2∠1
=2×180°-2×60°=240°;
故答案为:240°.
点评 本题考查了三角形的外角性质、对顶角相等以及三角形内角和定理;熟练掌握三角形的外角性质以及三角形内角和定理是解决问题的关键.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
17.已知二次函数y=ax2+bx+c的y与x的部分对应值如下表:则下列判断中正确的是( )
| x | … | -2 | 0 | 1 | 2 | … |
| y | … | 7 | -1 | -2 | -1 | … |
| A. | 抛物线开口向下 | B. | 抛物线的对称轴是y轴 | ||
| C. | x<1时,y随x的增大而减小 | D. | 抛物线与y轴交于正半轴 |
14.下列各式是最简二次根式的是( )
| A. | $\sqrt{12}$ | B. | $\sqrt{{x}^{2}+1}$ | C. | $\sqrt{0.5}$ | D. | $\sqrt{\frac{5}{3}}$ |
18.小李有2根木棒,长度分别为10cm和15cm,要组成一个三角形(木棒的首尾分别相连接),还需在下列4根木棒中选取( )
| A. | 4cm长的木棒 | B. | 5cm长的木棒 | C. | 20cm长的木棒 | D. | 25cm长的木棒 |
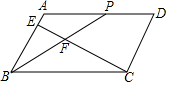 已知,如图?ABCD中,AB=5,BP平分∠ABC,CE⊥AB,垂足为E点,交BP于F点,若tan∠PFC=$\frac{4}{3}$,则BP=8.
已知,如图?ABCD中,AB=5,BP平分∠ABC,CE⊥AB,垂足为E点,交BP于F点,若tan∠PFC=$\frac{4}{3}$,则BP=8.