题目内容
9.已知关于x的二次函数y=x2-2mx+m2+m的图象与直线y=kx+1,若k=1,求证:无论m为何值,二次函数图象与直线总有两个不同的交点.分析 令k=1,联立y=x2-2mx+m2+m和y=x+1可得x2-(2m+1)x+m2+m-1=0,求出方程的根的判别式,进而结论可证明.
解答 证明:∵关于x的二次函数y=x2-2mx+m2+m的图象与直线y=kx+1,其中k=1,
∴x2-2mx+m2+m=x+1,即x2-(2m+1)x+m2+m-1=0,
∴△=(2m+1)2-4(m2+m-1),即△=5>0,
∴方程x2-(2m+1)x+m2+m-1=0,有两不相等的实数根,
∴无论m为何值,二次函数图象与直线总有两个不同的交点.
点评 本题主要考查了二次函数的性质,解答本题的关键是熟练掌握根的判别式的求法,此题难度不大.

练习册系列答案
相关题目
19.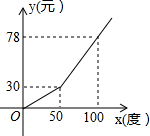 某地电力公司的用电收费标准如图,x(度)表示用户每月的用电量,y(元)表示每月应付的电费,看图可知,当用户一个月的用电量超过50度时,超过部分的收费标准是每度( )
某地电力公司的用电收费标准如图,x(度)表示用户每月的用电量,y(元)表示每月应付的电费,看图可知,当用户一个月的用电量超过50度时,超过部分的收费标准是每度( )
 某地电力公司的用电收费标准如图,x(度)表示用户每月的用电量,y(元)表示每月应付的电费,看图可知,当用户一个月的用电量超过50度时,超过部分的收费标准是每度( )
某地电力公司的用电收费标准如图,x(度)表示用户每月的用电量,y(元)表示每月应付的电费,看图可知,当用户一个月的用电量超过50度时,超过部分的收费标准是每度( )| A. | 0.96元 | B. | 0.78元 | C. | 0.60元 | D. | 0.3元 |
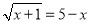 的解是( )
的解是( )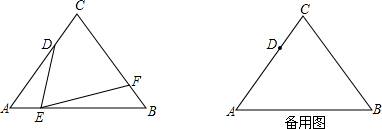
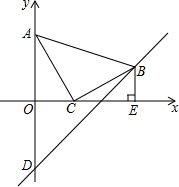 在平面直角坐标系中,现将一块等腰直角三角板ABC放在第一象限,斜靠在两条坐标轴上,且点A(0,2),点C(1,0),BE⊥x轴于点E,一次函数y=x+b经过点B,交y轴于点D.
在平面直角坐标系中,现将一块等腰直角三角板ABC放在第一象限,斜靠在两条坐标轴上,且点A(0,2),点C(1,0),BE⊥x轴于点E,一次函数y=x+b经过点B,交y轴于点D.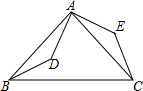 如图,点D是等腰直角三角形ABC内一点,AB=AC,将△ABD绕点A逆时针旋转90°,点D与点E重合,则△ABD≌△ACE;若连结DE,AD=3,则DE=3$\sqrt{2}$.
如图,点D是等腰直角三角形ABC内一点,AB=AC,将△ABD绕点A逆时针旋转90°,点D与点E重合,则△ABD≌△ACE;若连结DE,AD=3,则DE=3$\sqrt{2}$.