题目内容
16. 如图,在反比例函数y=$\frac{4}{x}$(x≥0)的图象上,有点P1,P2,P3,P4,…,Pn(n为正整数,且n≥1),它们的横坐标依次为1,2,3,4,…,n(n为正整数,且n≥1).分别过这些点作x轴与y轴的垂线,连接相邻两点,图中所构成的阴影部分(近似看成三角形)的面积从左到右依次为S1,S2,S3,…,Sn-1(n为正整数,且n≥2),那么S1+S2+S3+S4+S5=$\frac{8}{5}$.
如图,在反比例函数y=$\frac{4}{x}$(x≥0)的图象上,有点P1,P2,P3,P4,…,Pn(n为正整数,且n≥1),它们的横坐标依次为1,2,3,4,…,n(n为正整数,且n≥1).分别过这些点作x轴与y轴的垂线,连接相邻两点,图中所构成的阴影部分(近似看成三角形)的面积从左到右依次为S1,S2,S3,…,Sn-1(n为正整数,且n≥2),那么S1+S2+S3+S4+S5=$\frac{8}{5}$.
分析 求出P1、P2、P3、P4…的纵坐标,从而可计算出S1、S2、S3、S4…的高,进而求出S1、S2、S3、S4…,从而得出S1+S2+S3+S4+S5的值.
解答 解:当x=1时,P1的纵坐标为4,
当x=2时,P2的纵坐标为2,
当x=3时,P3的纵坐标为$\frac{4}{3}$,
当x=4时,P4的纵坐标为1,
当x=5时,P5的纵坐标为$\frac{4}{5}$
…
则S1=$\frac{1}{2}$×1×(4-2)=1=2-1;
S2=$\frac{1}{2}$×1×(2-$\frac{4}{3}$)=$\frac{1}{3}$=1-$\frac{2}{3}$;
S3=$\frac{1}{2}$×1×($\frac{4}{3}$-1)=$\frac{1}{6}$=$\frac{2}{3}$-$\frac{2}{4}$;
∴S1+S2+S3=2-1+1-$\frac{2}{3}$+$\frac{2}{3}$-$\frac{2}{4}$=2-$\frac{2}{4}$=$\frac{3}{2}$;
S4=$\frac{1}{2}$×1×(1-$\frac{4}{5}$)=$\frac{1}{10}$=$\frac{2}{4}$-$\frac{2}{5}$;
…
S5=$\frac{2}{5-1}$-$\frac{2}{5}$;
∴S1+S2+S3+S4+S5
=2-1+1-$\frac{2}{3}$+$\frac{2}{3}$-$\frac{2}{4}$+$\frac{2}{4}$-$\frac{2}{5}$=2-$\frac{2}{5}=\frac{8}{5}$.
故答案为$\frac{8}{5}$.
点评 此题考查了反比例函数图象上点的坐标特征,根据坐标求出个阴影的面积表达式是解题的关键.

 如图,AB∥PD,∠PAB=65°,∠PBA=78°,则∠APB的大小为( )
如图,AB∥PD,∠PAB=65°,∠PBA=78°,则∠APB的大小为( )| A. | 71.5° | B. | 39° | C. | 37° | D. | 32.5° |
 如图,BE=AD,AB=BC,BP为一条射线,AD⊥BP,CE⊥PB,若BD=6.求EC的长.
如图,BE=AD,AB=BC,BP为一条射线,AD⊥BP,CE⊥PB,若BD=6.求EC的长.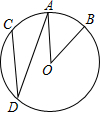 如图,点A,B,C,D分别在⊙O上,$\widehat{AB}$=$\widehat{AC}$,若∠AOB=40°,则∠ADC的大小是20度.
如图,点A,B,C,D分别在⊙O上,$\widehat{AB}$=$\widehat{AC}$,若∠AOB=40°,则∠ADC的大小是20度. 如图,菱形ABCD的周长为48cm,对角线AC、BD相交于O点,E是AD的中点,连接OE,则线段OE的长等于6cm.
如图,菱形ABCD的周长为48cm,对角线AC、BD相交于O点,E是AD的中点,连接OE,则线段OE的长等于6cm. 如图,在△ABC中,BD,CE分别为AC,AB边上的中线,BD⊥CE.若BD=3,CE=2,则△ABC的面积为( )
如图,在△ABC中,BD,CE分别为AC,AB边上的中线,BD⊥CE.若BD=3,CE=2,则△ABC的面积为( )