题目内容
8.规定一个虚数i,满足i2=-1.如i3=-i,i4=1,则(2i)5=32i.分析 根据积的乘方的性质展开,再根据同底数幂相乘,底数不变指数相加进行计算即可得解.
解答 解:(2i)5=32•i5
=32•i4•i
=32×1×i
=32i.
故答案为:32i.
点评 本题考查了幂的乘方与积的乘方,同底数幂的乘法,读懂题目信息,理解虚数单位的乘方规律的变化是解题的关键.

练习册系列答案
相关题目
20.若实数n满足(n-46)2+(45-n)2=2,则代数式(n-46)(45-n)的值是( )
| A. | -1 | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | 1 |
18.计算(-3x2y)2的结果是( )
| A. | -3x4y2 | B. | -9x4y2 | C. | 9x4y2 | D. | 9x4y |
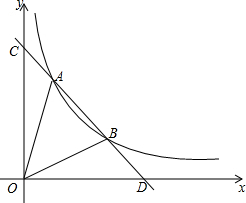 如图,一次函数的图形与y轴、x轴交于C、D两点,与反比例函数y=$\frac{6}{x}$(x>0)的图象交于A、B两点,且AB=2BD,则△AOB的面积为8.
如图,一次函数的图形与y轴、x轴交于C、D两点,与反比例函数y=$\frac{6}{x}$(x>0)的图象交于A、B两点,且AB=2BD,则△AOB的面积为8.