题目内容
在一个口袋中有4个完全相同的小球,把它们分别标号 1、2、3、4.小明先随机地摸出一个小球不放回,小强再随机地摸出一个小球.记小明摸出球的标号为x,小强摸出的球标号为y.小明和小强在此基础上共同协商一个游戏规则:当x>y 时小明获胜,否则小强获胜.
①用列表法或画树状图的方法,求小明获胜的概率.
②请问他们制定的游戏规则公平吗?试说明理由.
①用列表法或画树状图的方法,求小明获胜的概率.
②请问他们制定的游戏规则公平吗?试说明理由.
考点:游戏公平性,列表法与树状图法
专题:
分析:①首先根据题意画出树状图,由树状图求得所有等可能的结果与小明获胜的情况,继而利用概率公式即可求得答案,注意此题属于不放回实验;
②利用①中所求,进而得出两人获胜的概率.
②利用①中所求,进而得出两人获胜的概率.
解答:解:①画树状图得:

∵共有12种等可能的结果,小明获胜的有(2,1),(3,1),(3,2),(4,1),(4,2),(4,3)共6种情况,
∴小明获胜的概率为:
=
;
②他们制定的游戏规则公平,
∵小明和小强获胜的概率都为
,
∴他们制定的游戏规则公平.

∵共有12种等可能的结果,小明获胜的有(2,1),(3,1),(3,2),(4,1),(4,2),(4,3)共6种情况,
∴小明获胜的概率为:
| 6 |
| 12 |
| 1 |
| 2 |
②他们制定的游戏规则公平,
∵小明和小强获胜的概率都为
| 1 |
| 2 |
∴他们制定的游戏规则公平.
点评:本题考查的是游戏公平性的判断.判断游戏公平性就要计算每个事件的概率,概率相等就公平,否则就不公平.

练习册系列答案
相关题目
某外贸公司要出口一批食品罐头,标准质量为每听450克,现抽取10听样品进行检测,它们的质量与标准质量的差值(单位:克)如下:-10,+5,0,+5,0,0,-5,0,+5,+10,则这10听罐头质量的众数为( )
| A、460 | B、455 |
| C、450 | D、0 |
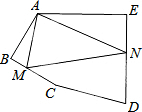 如图,在五边形ABCDE中,∠BAE=120°,∠B=∠E=90°,AB=BC,AE=DE,在BC、DE上分别找一点M、N,使得△AMN的周长最小时,则∠AMN+∠ANM的度数为( )
如图,在五边形ABCDE中,∠BAE=120°,∠B=∠E=90°,AB=BC,AE=DE,在BC、DE上分别找一点M、N,使得△AMN的周长最小时,则∠AMN+∠ANM的度数为( )| A、90° | B、100° |
| C、110° | D、120° |
不能判定两个直角三角形全等的条件是( )
| A、两个锐角对应相等 |
| B、两条直角边对应相等 |
| C、斜边和一锐角对应相等 |
| D、斜边和一条直角边对应相等 |
 如图,在平面直角坐标系中,A(6,0)、B(6,2)、C(0,2)、D(1,2),点P为线段OA上一点,且∠BPD=90°,则点P的坐标为
如图,在平面直角坐标系中,A(6,0)、B(6,2)、C(0,2)、D(1,2),点P为线段OA上一点,且∠BPD=90°,则点P的坐标为 如图是一个经过改造的台球桌面的示意图,图中四个角上的黑色部分分别表示四个人球孔.如果一个球按图中所示的方向被击出(球可以经过多次反弹),那么该球最后将落入的球袋是
如图是一个经过改造的台球桌面的示意图,图中四个角上的黑色部分分别表示四个人球孔.如果一个球按图中所示的方向被击出(球可以经过多次反弹),那么该球最后将落入的球袋是