题目内容
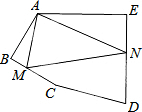 如图,在五边形ABCDE中,∠BAE=120°,∠B=∠E=90°,AB=BC,AE=DE,在BC、DE上分别找一点M、N,使得△AMN的周长最小时,则∠AMN+∠ANM的度数为( )
如图,在五边形ABCDE中,∠BAE=120°,∠B=∠E=90°,AB=BC,AE=DE,在BC、DE上分别找一点M、N,使得△AMN的周长最小时,则∠AMN+∠ANM的度数为( )| A、90° | B、100° |
| C、110° | D、120° |
考点:轴对称-最短路线问题
专题:
分析:根据要使△AMN的周长最小,即利用点的对称,让三角形的三边在同一直线上,作出A关于BC和ED的对称点A′,A″,即可得出∠AA′M+∠A″=∠HAA′=60°,进而得出∠AMN+∠ANM=2(∠AA′M+∠A″)即可得出答案.
解答: 解:作A关于BC和ED的对称点A′,A″,连接A′A″,交BC于M,交ED于N,则A′A″即为△AMN的周长最小值.作DA延长线AH,
解:作A关于BC和ED的对称点A′,A″,连接A′A″,交BC于M,交ED于N,则A′A″即为△AMN的周长最小值.作DA延长线AH,
∵∠DAE=120°,
∴∠HAA′=60°,
∴∠A′+∠A″=∠HAA′=60°,
∵∠A′=∠MAA′,∠NAE=∠A″,
且∠A′+∠MAA′=∠AMN,∠NAE+∠A″=∠ANM,
∴∠AMN+∠ANM=∠A′+∠MAA′+∠NAE+∠A″=2(∠A′+∠A″)=2×60°=120°,
故选:D.
 解:作A关于BC和ED的对称点A′,A″,连接A′A″,交BC于M,交ED于N,则A′A″即为△AMN的周长最小值.作DA延长线AH,
解:作A关于BC和ED的对称点A′,A″,连接A′A″,交BC于M,交ED于N,则A′A″即为△AMN的周长最小值.作DA延长线AH,∵∠DAE=120°,
∴∠HAA′=60°,
∴∠A′+∠A″=∠HAA′=60°,
∵∠A′=∠MAA′,∠NAE=∠A″,
且∠A′+∠MAA′=∠AMN,∠NAE+∠A″=∠ANM,
∴∠AMN+∠ANM=∠A′+∠MAA′+∠NAE+∠A″=2(∠A′+∠A″)=2×60°=120°,
故选:D.
点评:此题主要考查了平面内最短路线问题求法以及三角形的外角的性质和垂直平分线的性质等知识,根据已知得出M,N的位置是解题关键.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案
相关题目
数字24.6万精确到( )
| A、十分位 | B、个位 | C、千位 | D、万位 |
下列的运算中,其结果正确的是( )
A、3
| ||||||
| B、16x2-7x2=9x2 | ||||||
| C、x8÷x2=x4 | ||||||
| D、x(-xy)2=x2y2 |
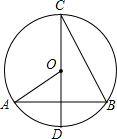 如图,在⊙O中,直径CD垂直弦AB,连接OA,CB,已知⊙O的半径为2,AB=2
如图,在⊙O中,直径CD垂直弦AB,连接OA,CB,已知⊙O的半径为2,AB=2| 3 |
| A、20° | B、30° |
| C、60° | D、70° |
将Rt△ABC的三边分别扩大2倍,得到Rt△A′B′C′,则( )
| A、sinA=sinA′ |
| B、sinA>sinA′ |
| C、sinA<sinA′ |
| D、不能确定 |
 解不等式组,并把它的解集在数轴上表示出来.
解不等式组,并把它的解集在数轴上表示出来.