题目内容
已知正n边形的一个外角与一个内角的比为1﹕3,则n等于( )
| A、4 | B、6 | C、8 | D、12 |
考点:多边形内角与外角
专题:
分析:设外角为x°,则其内角为3x°,根据其内外角互补可以列出方程求得外角的度数,然后利用外角和定理求得边数即可.
解答:解:设外角为x°,则其内角为3x°,
则x+3x=180,
解得:x=45,
∵正n边形外角和为360°,
∴n=360÷45=8
故选:C.
则x+3x=180,
解得:x=45,
∵正n边形外角和为360°,
∴n=360÷45=8
故选:C.
点评:本题考查了正多边形的外角与内角的知识,熟练掌握正多边形的内角和和外角和定理是解决此类题目的关键.

练习册系列答案
相关题目
如果把分式
中的x、y同时缩小为原来的一半,则分式的值( )
| xy |
| 2x+3y |
| A、不变 |
| B、缩小为原来的一半 |
| C、缩小为原来的四分之一 |
| D、扩大为原来的2倍 |
代数式a2+b2的意义是( )
| A、a的平方与b的和 |
| B、a与b的平方的和 |
| C、a与b两数的平方和 |
| D、a与b的和的平方 |
已知点A(-2,y1),B(-1,y2)和C(3,y3)都在反比例函数y=
的图象上,则y1、y2、y3的大小关系是( )
| 3 |
| x |
| A、y1<y2<y3 |
| B、y3<y2<y1 |
| C、y2<y1<y3 |
| D、y1<y3<y2 |
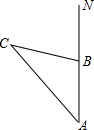 如图,一艘船从港口A处出发,以20海里/时的速度向正北方向航行,该船经过4小时到达B处,港口A北偏西35°方向上有一小岛C,轮船在B处观测到小岛C在北偏西70°的方向上,求从B处到小岛C的距离.
如图,一艘船从港口A处出发,以20海里/时的速度向正北方向航行,该船经过4小时到达B处,港口A北偏西35°方向上有一小岛C,轮船在B处观测到小岛C在北偏西70°的方向上,求从B处到小岛C的距离. 如图,已知矩形DEFG内接于△ABC,点D在AB上,点G在AC上,E、F在BC上,AH⊥BC于H,且交DG于N,BC=18cm,AH=6cm,DE:DG=2:3,求矩形DEFG的面积.
如图,已知矩形DEFG内接于△ABC,点D在AB上,点G在AC上,E、F在BC上,AH⊥BC于H,且交DG于N,BC=18cm,AH=6cm,DE:DG=2:3,求矩形DEFG的面积. 将一副三角板如图所示放在一起,连接AD,则∠ADB的正切值是
将一副三角板如图所示放在一起,连接AD,则∠ADB的正切值是 如图,E,F分别是线段AB,AC上的点,连结BF,CE,它们相交于点D,连结AD.若∠1=∠2,∠C=∠B,则图中有
如图,E,F分别是线段AB,AC上的点,连结BF,CE,它们相交于点D,连结AD.若∠1=∠2,∠C=∠B,则图中有 如图,某登山队从营地a出发,先在坡度(斜坡与水平线的夹角)为30°的AB坡攀登,然后沿坡度为45°的BC坡攀登,已知AB=100m,BC=200m,求这次登山队从营地A到山顶C的攀登垂直高度CD(精确到米,根号2≈1.414,根号3≈1.732)
如图,某登山队从营地a出发,先在坡度(斜坡与水平线的夹角)为30°的AB坡攀登,然后沿坡度为45°的BC坡攀登,已知AB=100m,BC=200m,求这次登山队从营地A到山顶C的攀登垂直高度CD(精确到米,根号2≈1.414,根号3≈1.732)