题目内容
11.如表记录了甲、乙、丙、丁四名运动员参加男子跳高选拔赛成绩的平均数x与方差S2:| 甲 | 乙 | 丙 | 丁 | |
| 平均数x(cm) | 175 | 173 | 175 | 174 |
| 方差S2(cm2) | 3.5 | 3.5 | 12.5 | 15 |
分析 首先比较平均数,平均数相同时选择方差较小的运动员参加.
解答 解:∵$\overline{{x}_{甲}}$=$\overline{{x}_{丙}}$>$\overline{{x}_{丁}}$>$\overline{{x}_{乙}}$,
∴从甲和丙中选择一人参加比赛,
∵$\overline{{{s}_{甲}}^{2}}$<$\overline{{{s}_{丙}}^{2}}$,
∴选择甲参赛,
故答案为:甲.
点评 此题考查了平均数和方差;熟练掌握平均数和方差的应用是解决问题的关键;方差反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
19. 如图,直线l1,l2,l3交于一点,直线l4∥l1,若∠1=36°,∠2=56°,则∠3的度数为( )
如图,直线l1,l2,l3交于一点,直线l4∥l1,若∠1=36°,∠2=56°,则∠3的度数为( )
 如图,直线l1,l2,l3交于一点,直线l4∥l1,若∠1=36°,∠2=56°,则∠3的度数为( )
如图,直线l1,l2,l3交于一点,直线l4∥l1,若∠1=36°,∠2=56°,则∠3的度数为( )| A. | 92° | B. | 88° | C. | 56° | D. | 36° |
6.某种计算机完成一次基本运算的时间约为1纳秒(μm),即0.000000001s,这个数用科学记数法表示为( )
| A. | 1×10-8s | B. | 1×10-9s | C. | 10×10-10s | D. | 0.1×10-8s |
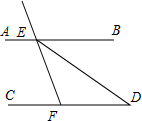 如图,若∠EFD=110°,∠FED=35°,ED平分∠BEF,那么AB与CD平行吗?请说明你的理由.
如图,若∠EFD=110°,∠FED=35°,ED平分∠BEF,那么AB与CD平行吗?请说明你的理由.