题目内容
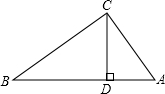 已知CD⊥AB,AC2=AD•AB,求证:
已知CD⊥AB,AC2=AD•AB,求证:(1)CD2=AD•BD;
(2)△ABC是直角三角形.
考点:相似三角形的判定与性质
专题:证明题
分析:(1)根据AC2=AD•AB,可证明△ACD∽△ABC,从而得出∠ACD=∠ABC,可证明△ACD∽△CBD,从而得出CD2=AD•BD;
(2)由(1)得△ACD∽△ABC,从而得出∠ACB=90°,则△ABC是直角三角形.
(2)由(1)得△ACD∽△ABC,从而得出∠ACB=90°,则△ABC是直角三角形.
解答:证明:(1)∵AC2=AD•AB,
∴
=
,
∵∠CAD=∠BAC,
∴△ACD∽△ABC,
∴∠ACD=∠ABC,
∴△ACD∽△CBD,
∴
=
,
∴CD2=AD•BD;
(2)由(1)得△ACD∽△ABC,
∴∠ADC=∠ACB,
∵CD⊥AB,
∴∠ADC=90°,
∴∠ACB=90°,
∴△ABC是直角三角形.
∴
| AC |
| AB |
| AD |
| AC |
∵∠CAD=∠BAC,
∴△ACD∽△ABC,
∴∠ACD=∠ABC,
∴△ACD∽△CBD,
∴
| CD |
| BD |
| AD |
| CD |
∴CD2=AD•BD;
(2)由(1)得△ACD∽△ABC,
∴∠ADC=∠ACB,
∵CD⊥AB,
∴∠ADC=90°,
∴∠ACB=90°,
∴△ABC是直角三角形.
点评:本题考查了相似三角形的判定和性质,判定两个三角形相似的方法有:三边对应成比例两个三角形相似;两边对应成比例,夹角相等,两个三角形相似;两角对应相等,两个三角形相似.

练习册系列答案
相关题目
 一个正方体的平面展开图如图,将它折成正方体后,“建”字的对面是( )
一个正方体的平面展开图如图,将它折成正方体后,“建”字的对面是( )| A、和 | B、谐 | C、海 | D、南 |
某校九年级8位同学一分钟跳绳的次数排序后如下:150,164,168,168,172,176,183,185.则由这组数据得到的结论中错误的是( )
| A、中位数为170 |
| B、众数为168 |
| C、极差为35 |
| D、平均数为171 |
 如图,若AB是⊙O的直径,CD是⊙O的弦,∠ABD=60°,则∠BCD=
如图,若AB是⊙O的直径,CD是⊙O的弦,∠ABD=60°,则∠BCD=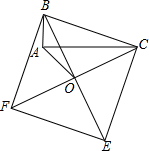 如图,以Rt△ABC的斜边BC为一边在△ABC的同侧作正方形BCEF,设正方形的中心为O,连结A0.如果AB=3,AO=2,那么AC的长等于
如图,以Rt△ABC的斜边BC为一边在△ABC的同侧作正方形BCEF,设正方形的中心为O,连结A0.如果AB=3,AO=2,那么AC的长等于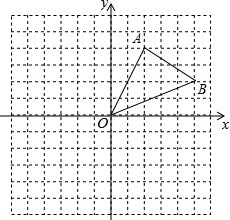 如图,三角形AOB中,A,B两点的坐标分别为(2,4)、(5,2).
如图,三角形AOB中,A,B两点的坐标分别为(2,4)、(5,2).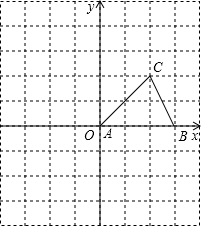 如图,△ABC的顶点A在原点,B、C坐标分别为B(3,0),C(2,2),将△ABC向左平移1个单位后再向下平移2单位,可得到△A′B′C′.
如图,△ABC的顶点A在原点,B、C坐标分别为B(3,0),C(2,2),将△ABC向左平移1个单位后再向下平移2单位,可得到△A′B′C′. 计算
计算 如图,D是△ABC的边AC上的一点,连接BD,已知∠ABD=∠C,AB=6,AD=4,求线段CD的长.
如图,D是△ABC的边AC上的一点,连接BD,已知∠ABD=∠C,AB=6,AD=4,求线段CD的长.