题目内容
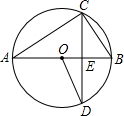 如图,AB是⊙O的直径,CD是弦,AB⊥CD垂足为点 E,连接OD、CB、AC,∠DOB=60°,EB=2,那么CD的长为( )
如图,AB是⊙O的直径,CD是弦,AB⊥CD垂足为点 E,连接OD、CB、AC,∠DOB=60°,EB=2,那么CD的长为( )A、
| ||
B、2
| ||
C、3
| ||
D、4
|
考点:垂径定理,含30度角的直角三角形,勾股定理
专题:
分析:根据同弧所对的圆周角等于所对圆心角的一半,可以容易求出∠BCE=30°,在直角三角形BCE中,利用含30°的直角三角形的性质和勾股定理算出CE的长,最后根据垂径定理求得CD的长
解答:解:∵∠DOB=60°,
∴∠BCE=30°.
在Rt△BCE中,∵BE=2,∠BCE=30°,
∴BC=4,CE=
=
=2
,
∵AB是⊙O的直径,AB⊥CD,
∴CE=DE=2
,
∴CD=4
=
=2
,
故选B.
∴∠BCE=30°.
在Rt△BCE中,∵BE=2,∠BCE=30°,
∴BC=4,CE=
| BC2-BE2 |
| 42-22 |
| 3 |
∵AB是⊙O的直径,AB⊥CD,
∴CE=DE=2
| 3 |
∴CD=4
| 3 |
| BC2-BE2 |
| 42-22 |
| 3 |
故选B.
点评:本题考查了垂径定理、含30°的直角三角形的性质,勾股定理等知识,是中考的常见题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
-
的倒数是( )
| 1 |
| 3 |
| A、3 | ||
B、
| ||
| C、-3 | ||
D、±
|
矩形具有而平行四边形不一定具有的特征是( )
| A、对角线互相平分 |
| B、对角线相等 |
| C、两组对角相等 |
| D、两组对边平行且相等 |
重庆一中初三年级某班10名同学的一次体考成绩如下表,则下列说法错误的是( )
| 成绩(分) | 39 | 42 | 44 | 45 | 48 | 50 |
| 人数 | 1 | 2 | 1 | 2 | 1 | 3 |
| A、这10名同学的平均成绩为45.5 |
| B、这10名同学成绩的中位数是45 |
| C、这10名同学成绩的众数为50 |
| D、这10名同学成绩的极差为2 |
下列各组数中,互为相反数的是( )
A、-2与-
| ||||||
B、|1-
| ||||||
C、
| ||||||
D、
|

 如图,AB=BC,以AB为直径的⊙O交AC于点D,过点D作DE⊥BC,垂足为E.
如图,AB=BC,以AB为直径的⊙O交AC于点D,过点D作DE⊥BC,垂足为E. 如图,矩形ABCD的对角线AC、BD相交于点O,AO=AD=2,以A为圆心,AO为半径作弧,则图中阴影部分的面积为
如图,矩形ABCD的对角线AC、BD相交于点O,AO=AD=2,以A为圆心,AO为半径作弧,则图中阴影部分的面积为