题目内容

Rt△ABC中，∠ABC=90°，AB=4，BC=3，若⊙O和三角形三边所在的直线都相切，则符合条件的⊙O的半径为
 
．
考点：三角形的内切圆与内心
专题：
分析：利用勾股定理求得斜边的长，根据直角三角形三边的长和内切圆的半径之间的关系求解．
解答：解：Rt△ABC的斜边BC=
AB2+BC2
=
42+32
=5，
则符合条件的⊙O的半径为：
3+4-5
2
=1．
故答案是：1．
点评：本题考查了直角三角形的内切圆，直角三角形的三边分别是a、b、c，其中c是斜边，则内切圆的半径是
a+b-c
2
．
练习册系列答案
相关题目
计算：-12+（2-π）0×|-2|+（-
1
3
）-2-
327
-2tan45°．
已知，△ABC的三个顶点A，B，C的坐标分别为A（4，0），B（0，-3），C（2，-4）．
（1）在如图的平面直角坐标系中画出△ABC，并分别写出点A，B，C关于x轴的对称点A′，B′，C′的坐标；
（2）将△ABC向左平移5个单位，请画出平移后的△A″B″C″，并写出△A″B″C″各个顶点的坐标．
（3）求出（2）中的△ABC在平移过程中所扫过的面积．
如图，正方形ABCD各顶点均在正方形EFGH的各边上（GB＜BF），且两正方形面积分别为25和49，则tan∠ABF=
 
．
如图，AC⊥CB，垂足为C点，AC=CB=8cm，点Q是AC的中点，动点P由B点出发，沿射线BC方向匀速移动．点P的运动速度为2cm/s．设动点P运动的时间为ts．为方便说明，我们分别记三角形ABC面积为S，三角形PCQ的面积为S1，三角形PAQ的面积为S2，三角形ABP的面积为S3．
（1）S3=
 
cm2（用含t的代数式表示）；
（2）当点P运动几秒，S1=
1
4
S，说明理由；
（3）请你探索是否存在某一时刻，使得S1=S2=S3？若存在，求出t值；若不存在，说明理由．
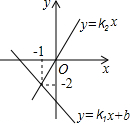同一平面直角坐标系中，一次函数y=k1x+b的图象与一次函数y=k2x的图象如图所示，则关于x的方程k1x+b=k2x的解为（　　）
A、x=0B、x=-1
C、x=-2D、x=1
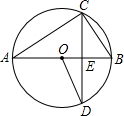如图，AB是⊙O的直径，CD是弦，AB⊥CD垂足为点 E，连接OD、CB、AC，∠DOB=60°，EB=2，那么CD的长为（　　）
A、
3
B、2
3
C、3
3
D、4
3
如图：已知线段AB=15cm，C点在AB上，BC=
2
3
AC，D为BC的中点，则线段AD的长是（　　）cm．
A、10B、13C、9D、12
如图，边长为a的正六边形内有一边长为a的正三角形，则
S阴影
S空白
=（　　）
A、3B、4C、5D、6

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网