题目内容
11．二次函数y=x2+2x的图象可能是（ ）| A． |  | B． |  | C． |  | D． |  |
分析 由二次函数性质知道其对称轴x=$\frac{-b}{2a}$=-1，当a＞0时，抛物线y=ax2+bx+c（a≠0）的开口向上，最后得到答案．
解答 解：∵二次函数y=x2+2x，
∴此二次函数图象的开口向上，对称轴是x=-1，
故选：C．
点评 本题考查了二次函数的性质：二次函数的称轴x=$\frac{-b}{2a}$；当a＞0时，抛物线y=ax2+bx+c（a≠0）的开口向上，x＜-$\frac{b}{2a}$时，y随x的增大而减小；x＞-$\frac{b}{2a}$时，y随x的增大而增大．
练习册系列答案
新课标阶梯阅读训练系列答案
口算心算速算应用题系列答案
相关题目
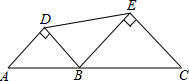如图，A、B、C三点在同一直线上，以AB、BC为斜边分别作等腰直角三角形ABD和BCE，连接DE．若AC=4，则DE的取值范围是2≤DE$＜2\sqrt{2}$．
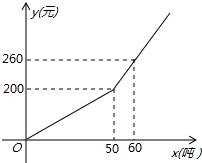已知某企业2014年用水量x（吨）与该月应交的水费y（元）之间的函数关系如图．
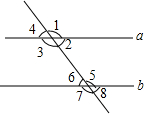如图所示，直线c截直线a，b，现给出下列以下条件：①∠4=∠8；②∠1=∠7；③∠2=∠6；④∠4+∠7=180°．其中能说明a∥b的条件有（ ）个．
1．把一枚六个面编号分别为1，2，3，4，5，6的质地均匀的正方体骰子先后投掷2次，若两个正面朝上的编号分别为m、n，则二次函数y=x2+mx+n的图象与x轴没有公共点的概率是（ ）
| A． | $\frac{5}{12}$ | B． | $\frac{4}{9}$ | C． | $\frac{17}{36}$ | D． | $\frac{1}{2}$ |