题目内容
20．在梯形ABCD中，AD∥BC，∠B=25°，∠C=65°，M，E，N，F分别是BC，BA，AD，DC的中点，若EF=4，MN=3，求BC．分析 作NG∥AB交BC于G，作NH∥CD交BC于H，根据平行四边形的性质得到BG=AN，CH=ND，∠NGH=∠B=25°，∠NHG=∠C=65°，得到∠GNH=90°，根据直角三角形的性质得到GH=2MN=6，根据梯形中位线定理得到答案．
解答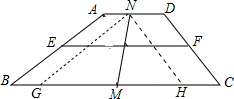 
解：作NG∥AB交BC于G，作NH∥CD交BC于H，
则四边形ABGN和四边形NHCD为平行四边形，
∴BG=AN，CH=ND，又AN=ND，
∴BG=CH，又BM=MC，
∴GM=MH，
∠NGH=∠B=25°，∠NHG=∠C=65°，
∴∠GNH=90°，又GM=MH，
∴GH=2MN=6，
∵AD+BC=2EF=8，
∴AD=1，
∴BC=GH+BG+HC=GH+AD=7．
点评 本题考查的是梯形的性质、梯形的中位线定理和直角三角形的性质，正确作出辅助线、掌握梯形的中位线平行于两底且等于两底和的一半是解题的关键．
练习册系列答案
相关题目
3．下列给出的点中，在函数y=-2x+1的图象上的点是（ ）
| A． | （1，3） | B． | （-2.5，-4） | C． | （2.5，-4） | D． | （-1，1） |
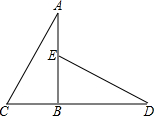已知：如图，AB⊥CD，垂足为B，点E在AB上，AB=BD，BE=BC，求证：△ABC≌△DBE．
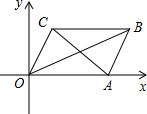如图，在平面直角坐标系xOy中，A（4，0），OA=OC，∠AOC=60°，且CB∥OA，OB平分∠AOC，点P是四边形OABC的内部一点，且点P到四边形OABC四条边的距离相等．
5．下列能用平方差公式计算的是（ ）
| A． | （a+1）（1+a） | B． | （$\frac{1}{2}$a+b）（b-$\frac{1}{2}$a） | C． | （-x+y）（x-y） | D． | （x2-y）（x+y2） |
12．
一个不等式组的解集在数轴上的表示如图，则这个不等式组的解集是（ ）
一个不等式组的解集在数轴上的表示如图，则这个不等式组的解集是（ ）| A． | -1＜x＜3 | B． | -1＜x≤3 | C． | -1≤x＜3 | D． | -1≤x≤3 |