题目内容
9. 在平面直角坐标系xOy中,抛物线y=-2x2+(m+9)x-6的对称轴是x=2.
在平面直角坐标系xOy中,抛物线y=-2x2+(m+9)x-6的对称轴是x=2.(1)求抛物线表达式和顶点坐标;
(2)将该抛物线向右平移1个单位,平移后的抛物线与原抛物线相交于点A,求点A的坐标;
(3)抛物线y=-2x2+(m+9)x-6与y轴交于点C,点A关于平移后抛物线的对称轴的对称点为点B,两条抛物线在点A、C和点A、B之间的部分(包含点A、B、C) 记为图象M.将直线y=2x-2向下平移b(b>0)个单位,在平移过程中直线与图象M始终有两个公共点,请你写出b的取值范围0<b≤$\frac{7}{2}$.
分析 (1)根据抛物线的对称轴公式求出m的值,进而求出抛物线的解析式以及顶点坐标;
(2)先求出平移后的抛物线解析式,然后求出交点坐标;
(3)根据图象即可写出b的取值范围.
解答 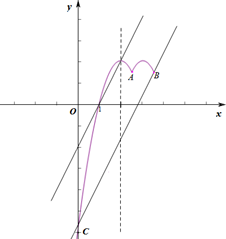 解:(1)∵抛物线y=-2x2+(m+9)x-6的对称轴是x=2,
解:(1)∵抛物线y=-2x2+(m+9)x-6的对称轴是x=2,
∴$-\frac{m+9}{2×(-2)}=2$.
∴m=-1.
∴抛物线的表达式为y=-2x2+8x-6.
∴y=-2(x-2)2+2.
∴顶点坐标为(2,2).
(2)由题意得,平移后抛物线表达式为y=-2(x-3)2+2,
∵-2(x-2)2=-2(x-3)2,
∴$x=\frac{5}{2}$.
∴A($\frac{5}{2}$,$\frac{3}{2}$).
(3)点A坐标为($\frac{5}{2}$,$\frac{3}{2}$),
则点B的坐标为($\frac{7}{2}$,$\frac{3}{2}$),
设直线y=2x-2向下平移b(b>0)个单位经过点B,
则y=2x-2-b,
故$\frac{3}{2}$=7-2-b,
解得b=$\frac{7}{2}$,
平移过程中直线与图象M始终有两个公共点,则$0<b≤\frac{7}{2}$.
点评 本题主要考查了二次函数的性质以及函数图象的几何变换,解题的关键是熟练掌握抛物线对称轴的求法以及数形结合解题思想.

练习册系列答案
相关题目
8.若分式$\frac{x+1}{x}$的值为0,则x的值为( )
| A. | 0 | B. | -1 | C. | 1 | D. | 2 |
9.下列m的取值中,能使抛物线y=x2+(2m-4)x+m-1顶点在第三象限的是( )
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
17.如图是“福娃欢欢”的五福图案,②、③、④、⑤中可以通过平移图案①得到的是( )


| A. | ② | B. | ③ | C. | ④ | D. | ⑤ |
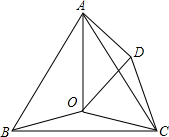 已知:如图,O是等边△ABC内一点,∠AOB=105°,将△BOC绕点C顺时针旋转使CB与CA重合,得到△ADC,连接OD.
已知:如图,O是等边△ABC内一点,∠AOB=105°,将△BOC绕点C顺时针旋转使CB与CA重合,得到△ADC,连接OD. 如图,△BCE是△ADB经过平移得到的,AD=4cm,BD=6cm,EB=7cm.求:
如图,△BCE是△ADB经过平移得到的,AD=4cm,BD=6cm,EB=7cm.求:

