题目内容
7．
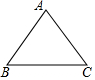如图，等腰△ABC的周长是36cm，底边为10cm，则底角的正切值是$\frac{12}{5}$．
分析 根据等腰三角形的性质得到BD=DC=$\frac{1}{2}$BC=5cm，AB=AC=13cm，根据勾股定理得到AD=12，由三角函数的定义即可得到结论．
解答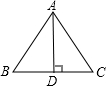 
解：∵AB=AC，AD是高，BC=10cm，
∴BD=DC=$\frac{1}{2}$BC=5cm，AB=AC=13cm，
在Rt△ADB中，
由勾股定理得：AB2=AD2+BD2，
∴AD=12cm，
∴tanC=$\frac{AD}{CD}$=$\frac{12}{5}$．
故答案为：$\frac{12}{5}$．
点评 本题考查了解直角三角形，等腰三角形的性质，勾股定理；熟练掌握等腰三角形的性质，作出图形是解题的关键．
练习册系列答案
相关题目
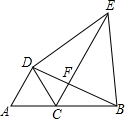如图，点C在线段AB上，△DAC和△DBE都是等边三角形．
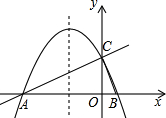如图，在平面直角坐标系xoy中，直线y=$\frac{1}{2}$x+2与x轴交于点A，与y轴交于点C，抛物线y=ax2+bx+c的对称轴是x=-$\frac{3}{2}$，且经过A，C两点，与x轴的另一个交点为点B．