题目内容
17.已知2a-1的平方根是±3,$\sqrt{(-16)^{2}}$的算术平方根是b,求$\sqrt{a+b}$值.分析 先依据平方根、算术平方根的定义得到a、b的值,然后再代入求解即可.
解答 解:∵2a-1的平方根是±3,
∴2a-1=9,
∴a=5,
∵$\sqrt{(-16)^{2}}$的算术平方根是b,且$\sqrt{(-16)^{2}}$=16,
即16的算术平方根是b,
∴b=4,
∴$\sqrt{a+b}$=$\sqrt{5+4}$=3.
点评 本题主要考查的是算术平方根和平方根的定义,由平方根和算术平方根的定义得到2a-1=9,b=4是解题的关键.

练习册系列答案
相关题目
7.下列式子计算正确的是( )
| A. | (-3)-(-6)=-9 | B. | -42=-16 | C. | $\sqrt{-4}$=-2 | D. | $\sqrt{9}$=±3 |
6.把抛物线y=-x2向左平移1个单位,然后向上平移3个单位,则平移后抛物线的解析式为( )
| A. | y=-(x-1)2+3 | B. | y=-(x+1)2+3 | C. | y=-(x+1)2-3 | D. | y=-(x-1)2-3 |
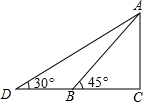 如图,幼儿园为了加强安全管理,决定将园内的滑滑梯的倾角由45°降为30°,已知原滑滑梯AB的长为5m,点D,B,C在同一水平地面上.
如图,幼儿园为了加强安全管理,决定将园内的滑滑梯的倾角由45°降为30°,已知原滑滑梯AB的长为5m,点D,B,C在同一水平地面上.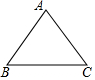 如图,等腰△ABC的周长是36cm,底边为10cm,则底角的正切值是$\frac{12}{5}$.
如图,等腰△ABC的周长是36cm,底边为10cm,则底角的正切值是$\frac{12}{5}$.