题目内容
20.已知x:y=3:5,y:z=2:3,求$\frac{x+y+z}{2x-y+z}$的值.分析 根据比例的性质,可用y表示x,用y表示z,根据分式的性质,可得答案.
解答 解:∵x:y=3:5,y:z=2:3,
∴x=$\frac{3}{5}$y,z=$\frac{3}{2}$y,
∴$\frac{x+y+z}{2x-y+z}$=$\frac{\frac{3}{5}y+y+\frac{3}{2}y}{\frac{6}{5}y-y+\frac{3}{2}y}$=$\frac{31}{17}$.
点评 本题考查了比例的性质,利用比例的性质得出x=$\frac{3}{5}$y,z=$\frac{3}{2}$y是解题关键.

练习册系列答案
相关题目
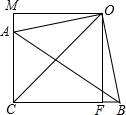 如图,Rt△ABC中,∠ACB=90°,以斜边AB为边向外作等腰Rt△ABO,AC=5,OC2=72,过点O作OF⊥BC于F,AM⊥OM于M,OM=CF.
如图,Rt△ABC中,∠ACB=90°,以斜边AB为边向外作等腰Rt△ABO,AC=5,OC2=72,过点O作OF⊥BC于F,AM⊥OM于M,OM=CF.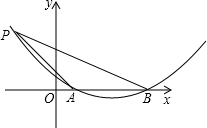 如图,已知抛物线y=ax2+bx+c与x轴交于A、B两点,AB=4,P是抛物线上一点,它的横坐标为-2,∠PAO=45°,cot∠PBO=$\frac{7}{3}$.
如图,已知抛物线y=ax2+bx+c与x轴交于A、B两点,AB=4,P是抛物线上一点,它的横坐标为-2,∠PAO=45°,cot∠PBO=$\frac{7}{3}$.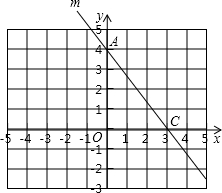 如图,直线m在坐标系中的图象经过点A(0,4)、C( 3,0),直线n经过点A和(-3,1)交x轴于点B.
如图,直线m在坐标系中的图象经过点A(0,4)、C( 3,0),直线n经过点A和(-3,1)交x轴于点B.