题目内容
计算(2+1)(22+1)(24+1)(28+1)(264+1)
考点:平方差公式
专题:
分析:先乘以2-1,再依次根据平方差公式进行计算,最后根据有理数的乘法求出即可.
解答:解:原式=(2-1)(2+1)(22+1)(24+1)(28+1)(264+1)
=(22-1)(22+1)(24+1)(28+1)(264+1)
=(24-1)(24+1)(28+1)(264+1)
=(28-1)(28+1)(264+1)
=(216-1)(264+1)
=280+216-264-1.
=(22-1)(22+1)(24+1)(28+1)(264+1)
=(24-1)(24+1)(28+1)(264+1)
=(28-1)(28+1)(264+1)
=(216-1)(264+1)
=280+216-264-1.
点评:本题考查了有理数的混合运算,平方差公式的应用,主要考查学生运用公式进行计算的能力,注意:(a+b)(a-b)=a2-b2,难度适中.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
若x=-1是方程2x-5a=3的解,则a的值为( )
| A、1 | B、-1 | C、2 | D、3 |
 如图,⊙O的直径AB垂直弦CD于M,且M是半径OB的中点,CD=2
如图,⊙O的直径AB垂直弦CD于M,且M是半径OB的中点,CD=2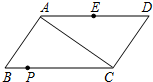 如图,已知?ABCD中,AB=30cm,AC=40cm,BC=50cm,边AD的中点为E,有一动点P从点B出发以1cm/秒的速度,沿边BC→CD运动至D点停止,若点P、E、C三点为顶点,构成以EP为腰的等腰△PEC时,运动时间为
如图,已知?ABCD中,AB=30cm,AC=40cm,BC=50cm,边AD的中点为E,有一动点P从点B出发以1cm/秒的速度,沿边BC→CD运动至D点停止,若点P、E、C三点为顶点,构成以EP为腰的等腰△PEC时,运动时间为