题目内容
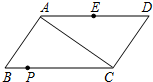 如图,已知?ABCD中,AB=30cm,AC=40cm,BC=50cm,边AD的中点为E,有一动点P从点B出发以1cm/秒的速度,沿边BC→CD运动至D点停止,若点P、E、C三点为顶点,构成以EP为腰的等腰△PEC时,运动时间为
如图,已知?ABCD中,AB=30cm,AC=40cm,BC=50cm,边AD的中点为E,有一动点P从点B出发以1cm/秒的速度,沿边BC→CD运动至D点停止,若点P、E、C三点为顶点,构成以EP为腰的等腰△PEC时,运动时间为考点:平行四边形的性质,等腰三角形的判定
专题:动点型
分析:根据勾股定理以及平行四边形的性质得出EH,FC的长,再利用当构成以EP为腰的等腰△PEC时有:①P1E=P1C,②P3E=CE,③P4E=P4C,④P6E=CE,进而得出答案.
解答:解: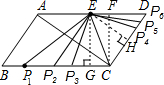 如图:
如图:
∵AB=30cm,AC=40cm,BC=50cm
∴AB2+AC2=BC2
∴△ABC和△ACD是Rt△
作CF⊥AB,EH⊥CD
∴△ACD∽△CFD
∴
=
=
,
∴FD=
=
=18,
FC=
=40×30÷50=24,
∵边AD的中点为E,
∴DE=25,
∴EF=DE-FD=25-18=7,
∴CE=
=25=CD,
∴CH=
CD=15,
∴EH=
=20(cm),
当构成以EP为腰的等腰△PEC时有:①P1E=P1C,②P3E=CE,③P4E=P4C,④P6E=CE
①P1E=P1C,
CG=EF=7,EG=CF=24,
∴在Rt△P1GE中有:(P1C-CG)2+EG2=P1E2
即:((P1C-7)2+242=P1C2
解得:P1C=
,
∴BP1=BC-P1C=50-
=
(cm),
∴t1=
÷1=
(s)
②P3E=CE时有P3C=2CG=2EF=14
∴BP3=BC-P3C=50-14=36
∴t2=36÷1=36(s)
③P4E=P4C时有:∵P4H2+EH2=P4E2
∴(P4C-15)2+202=P4C2
解得:P4C=
,
故t3=(BC+P4C)÷1=50+
=
(s)
④P6E=CE时有P6C=CD=30
∴t4=(BC+CD)÷1=80(s)
综上,当
秒或36秒或
秒或80秒时构成以EP为腰的等腰△PEC.
故答案为:
秒或36秒或
秒或80秒.
 如图:
如图:∵AB=30cm,AC=40cm,BC=50cm
∴AB2+AC2=BC2
∴△ABC和△ACD是Rt△
作CF⊥AB,EH⊥CD
∴△ACD∽△CFD
∴
| FD |
| DC |
| FC |
| AC |
| CD |
| AD |
∴FD=
| DC2 |
| AD |
| 302 |
| 50 |
FC=
| AC•DC |
| AD |
∵边AD的中点为E,
∴DE=25,
∴EF=DE-FD=25-18=7,
∴CE=
| CF2+EF2 |
∴CH=
| 1 |
| 2 |
∴EH=
| CE2-CH2 |
当构成以EP为腰的等腰△PEC时有:①P1E=P1C,②P3E=CE,③P4E=P4C,④P6E=CE
①P1E=P1C,
CG=EF=7,EG=CF=24,
∴在Rt△P1GE中有:(P1C-CG)2+EG2=P1E2
即:((P1C-7)2+242=P1C2
解得:P1C=
| 625 |
| 14 |
∴BP1=BC-P1C=50-
| 625 |
| 14 |
| 75 |
| 14 |
∴t1=
| 75 |
| 14 |
| 75 |
| 14 |
②P3E=CE时有P3C=2CG=2EF=14
∴BP3=BC-P3C=50-14=36
∴t2=36÷1=36(s)
③P4E=P4C时有:∵P4H2+EH2=P4E2
∴(P4C-15)2+202=P4C2
解得:P4C=
| 125 |
| 6 |
故t3=(BC+P4C)÷1=50+
| 125 |
| 6 |
| 425 |
| 6 |
④P6E=CE时有P6C=CD=30
∴t4=(BC+CD)÷1=80(s)
综上,当
| 75 |
| 14 |
| 425 |
| 6 |
故答案为:
| 75 |
| 14 |
| 425 |
| 6 |
点评:此题主要考查了平行四边形的性质以及勾股定理和等腰三角形的性质等知识,利用分类讨论得出是解题关键.

练习册系列答案
相关题目
下列图案中,既是轴对称图形又是中心对称图形的是( )
A、 |
B、 |
C、 |
D、 |
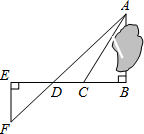 某地进行广场修建时,遇到了一个池塘,为了测量池塘隔开的A,B两点之间的距离.根据实际情况,作出如图所示的图形,其中AB⊥BE,EF⊥BE,AF交BE于D,
某地进行广场修建时,遇到了一个池塘,为了测量池塘隔开的A,B两点之间的距离.根据实际情况,作出如图所示的图形,其中AB⊥BE,EF⊥BE,AF交BE于D,