题目内容
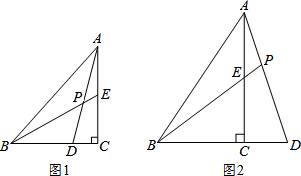
5. 已知:如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E,连接DE交AC于点F.
已知:如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E,连接DE交AC于点F.(1)求证:四边形ADCE为矩形;
(2)当△ABC满足什么条件时,四边形ADCE是一个正方形?并给出证明.
(3)在(2)的条件下,若AB=AC=2$\sqrt{2}$,求正方形ADCE周长.
分析 (1)根据等腰三角形的性质,可得∠CAD=$\frac{1}{2}$∠BAC,根据等式的性质,可得∠CAD+∠CAE=$\frac{1}{2}$(∠BAC+∠CAM)=90°,根据垂线的定义,可得∠ADC=∠CEA,根据矩形的判定,可得答案;
(2)根据等腰直角三角形的性质,可得AD与CD的关系,根据正方形的判定,可得答案;
(3)根据勾股定理,可得AD的长,根据正方形周长公式,可得答案.
解答 (1)证明:∵AB=AC,AD⊥BC,垂足为点D,
∴∠CAD=$\frac{1}{2}$∠BAC.
∵AN是△ABC外角∠CAM的平分线,
∴∠CAE=$\frac{1}{2}$∠CAM.
∵∠BAC与∠CAM是邻补角,
∴∠BAC+∠CAM=180°,
∴∠CAD+∠CAE=$\frac{1}{2}$(∠BAC+∠CAM)=90°.
∵AD⊥BC,CE⊥AN,
∴∠ADC=∠CEA=90°,
∴四边形ADCE为矩形;
(2)∠BAC=90°且AB=AC时,四边形ADCE是一个正方形,
证明:∵∠BAC=90°且AB=AC,AD⊥BC,
∴∠CAD=$\frac{1}{2}$∠BAC=45°,∠ADC=90°,
∴∠ACD=∠CAD=45°,
∴AD=CD.
∵四边形ADCE为矩形,
∴四边形ADCE为正方形;
(3)解:由勾股定理,得
$\sqrt{A{D}^{2}+C{D}^{2}}$=AB,AD=CD,
即$\sqrt{2}$AD=2$\sqrt{2}$,
AD=2,
正方形ADCE周长4AD=4×2=8.
点评 本题考查了的正方形的判定与性质,(1)利用了等腰三角形的性质,矩形的判定;(2)利用了正方形的判定;(3)利用了勾股定理,正方形的周长.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目
16.下列等式从左到右的变形,属于因式分解的是( )
| A. | m2+n2=(m+n)2 | B. | x2-1=x(x-$\frac{1}{x}$) | C. | a2-2a-1=(a-1)2-2 | D. | x2-4y2=(x-2y)(x+2y) |
17.下列计算正确的是( )
| A. | 2x+3x=6x2 | B. | 3x+4y=7xy | C. | 5x2-7x2=-2 | D. | 8x3y2-8y2x3=0 |




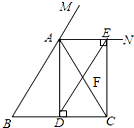
 如图,∠A=90°,∠D=90°,AC与BD相交于点E,BE=EC.
如图,∠A=90°,∠D=90°,AC与BD相交于点E,BE=EC.