题目内容
已知:|ab-2|+(b+1)2=0,求
+
+
+…+
的值.
| 1 |
| ab |
| 1 |
| (a-1)(b-1) |
| 1 |
| (a-2)(b-2) |
| 1 |
| (a-2012)(b-2012) |
分析:利用非负数的性质求出a与b的值,代入原式利用拆项法变形,计算即可得到结果.
解答:解:∵|ab-2|+(b+1)2=0,
∴ab-2=0,b+1=0,即a=-2,b=-1,
则原式=
+
+
+…+
=1-
+
-
+…+
-
=1-
=
.
∴ab-2=0,b+1=0,即a=-2,b=-1,
则原式=
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| 2013×2014 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2013 |
| 1 |
| 2014 |
| 1 |
| 2014 |
| 2013 |
| 2014 |
点评:此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
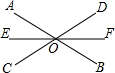 如图,已知直线AB、CD交于点O,OE平分∠AOC,OF平分∠BOD,
如图,已知直线AB、CD交于点O,OE平分∠AOC,OF平分∠BOD, 如图,已知直线AB、CD、MN相交于点O,∠1=22°,∠2=46°,求∠3的度数.
如图,已知直线AB、CD、MN相交于点O,∠1=22°,∠2=46°,求∠3的度数.