题目内容
17.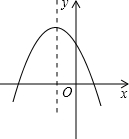 已知二次函数y=ax2+bx+c的图象如图所示,那么下列结论:
已知二次函数y=ax2+bx+c的图象如图所示,那么下列结论:①a<0,②b<0,③c<0,
其中正确的判断是( )
| A. | ①② | B. | ①③ | C. | ②③ | D. | ①②③ |
分析 利用抛物线开口方向可对①进行判断;利用对称轴的位置可对②进行判断;利用抛物线与y轴的交点位置可对③进行判断.
解答 解:∵抛物线开口向下,
∴a<0,所以①正确;
∵抛物线的对称轴在y轴的左侧,
∴b<0,所以②正确;
∵抛物线与y轴的交点在x轴上方,
∴c>0,所以③错误.
故选A.
点评 本题考查了二次函数图象于系数的关系:对于二次函数y=ax2+bx+c(a≠0),二次项系数a决定抛物线的开口方向和大小.当a>0时,抛物线向上开口;当a<0时,抛物线向下开口;一次项系数b和二次项系数a共同决定对称轴的位置:当a与b同号时(即ab>0),对称轴在y轴左; 当a与b异号时(即ab<0),对称轴在y轴右.(简称:左同右异);常数项c决定抛物线与y轴交点:抛物线与y轴交于(0,c).

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
7.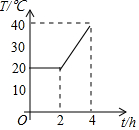 一个试验室在0:00-4:00的温度T(单位:℃)与时间t (单位:h)的函数关系的图象如图所示,在0:00-2:00保持恒温,在2:00-4:00匀速升温,则开始升温后试验室每小时升高的温度为( )
一个试验室在0:00-4:00的温度T(单位:℃)与时间t (单位:h)的函数关系的图象如图所示,在0:00-2:00保持恒温,在2:00-4:00匀速升温,则开始升温后试验室每小时升高的温度为( )
 一个试验室在0:00-4:00的温度T(单位:℃)与时间t (单位:h)的函数关系的图象如图所示,在0:00-2:00保持恒温,在2:00-4:00匀速升温,则开始升温后试验室每小时升高的温度为( )
一个试验室在0:00-4:00的温度T(单位:℃)与时间t (单位:h)的函数关系的图象如图所示,在0:00-2:00保持恒温,在2:00-4:00匀速升温,则开始升温后试验室每小时升高的温度为( )| A. | 5℃ | B. | 10℃ | C. | 20℃ | D. | 40℃ |
8.下列运算正确的是( )
| A. | a3+a2=2a5 | B. | 2a(1-a)=2a-2a2 | C. | (-ab2)3=a3b6 | D. | (a+b)2=a2+b2 |
5.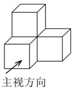 如图是由四个相同的小正方体组成的立体图形,它的主视图是( )
如图是由四个相同的小正方体组成的立体图形,它的主视图是( )
 如图是由四个相同的小正方体组成的立体图形,它的主视图是( )
如图是由四个相同的小正方体组成的立体图形,它的主视图是( )| A. |  | B. | 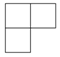 | C. |  | D. |  |
12.下列计算正确的是( )
| A. | a+a=a2 | B. | a•a2=a3 | C. | (-a3)2=a9 | D. | (3a)3=9a3 |
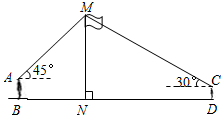 如图,某数学兴趣小组在活动课上测量学校旗杆高度.已知小明的眼睛与地面的距离AB=1.7m,看旗杆顶部M的仰角为45°;小红的眼睛与地面的距离CD=1.5m,看旗杆顶部M的仰角为30°.两人相距28米且位于旗杆两侧(点B、N、D在同一条直线上).请求出旗杆MN的高度.(参考数据:$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7,结果保留整数)
如图,某数学兴趣小组在活动课上测量学校旗杆高度.已知小明的眼睛与地面的距离AB=1.7m,看旗杆顶部M的仰角为45°;小红的眼睛与地面的距离CD=1.5m,看旗杆顶部M的仰角为30°.两人相距28米且位于旗杆两侧(点B、N、D在同一条直线上).请求出旗杆MN的高度.(参考数据:$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7,结果保留整数)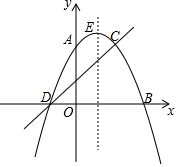 如图,抛物线y=ax2+bx+c过A(0,4),B(4,0),C(2,4)三点,与x轴另一交点记作D,直线y=kx+n过C、D两点.
如图,抛物线y=ax2+bx+c过A(0,4),B(4,0),C(2,4)三点,与x轴另一交点记作D,直线y=kx+n过C、D两点.