题目内容
17.已知x=2+$\sqrt{3}$,y=2-$\sqrt{3}$,求$\sqrt{x}+\sqrt{y}$的值.分析 由x=2+$\sqrt{3}$=$\frac{1}{2}$($\sqrt{3}$+1)2,y=2-$\sqrt{3}$=$\frac{1}{2}$($\sqrt{3}$-1)2,进一步代入开方求得答案即可.
解答 解:∵x=2+$\sqrt{3}$=$\frac{1}{2}$($\sqrt{3}$+1)2,y=2-$\sqrt{3}$=$\frac{1}{2}$($\sqrt{3}$-1)2,
∴$\sqrt{x}+\sqrt{y}$=$\frac{\sqrt{2}}{2}$($\sqrt{3}$+1)+$\frac{\sqrt{2}}{2}$($\sqrt{3}$-1)=$\sqrt{6}$.
点评 此题考查二次根式的化简求值,利用完全平方公式把x、y的值变形是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.下列各数中,不是有理数的数是( )
| A. | 3.1415926 | B. | -$\frac{22}{7}$ | C. | π | D. | -6.$\stackrel{•}{3}$0$\stackrel{•}{7}$ |

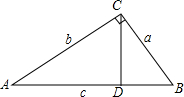 如图,△ABC中,∠ACB=90°,AB=c,BC=a,AC=b,且(c-$\sqrt{8}$)2+|$\sqrt{2}$-a|=0.
如图,△ABC中,∠ACB=90°,AB=c,BC=a,AC=b,且(c-$\sqrt{8}$)2+|$\sqrt{2}$-a|=0.