题目内容
已知矩形ABCD中,AB=8,AD=6,点M、N分别是对角线BD和边BC上的动点,则CM+MN的最小值为 .
考点:轴对称-最短路线问题,矩形的性质
专题:
分析:根据轴对称求最短路线的方法得出M点位置,进而利用等边三角形的性质与判定以及锐角三角函数关系求出MC+NM的值.
解答: 解:如图所示:由题意可得出:作C点关于BD对称点C′,连接BC′,
解:如图所示:由题意可得出:作C点关于BD对称点C′,连接BC′,
过点C′作C′N⊥BC于点N,交BD于点M,连接MC,此时CM+NM=C′N最小.
设 BN=x,NC=(6-x),
由相似三角形的性质,得
MN:8=x:6,
解得MN=
x.
由勾股定理,得
MC2=
x2-12x+36.
MC′2=MC=
x2-12x+36.
NC′2=
x2-
x+36.
由勾股定理,得BC′2-BN2=C′N2,
即62-x2=
x2-
x+36,
解得:x=6,
所以CM+NM=C′N=
,
故答案为:
.
 解:如图所示:由题意可得出:作C点关于BD对称点C′,连接BC′,
解:如图所示:由题意可得出:作C点关于BD对称点C′,连接BC′,过点C′作C′N⊥BC于点N,交BD于点M,连接MC,此时CM+NM=C′N最小.
设 BN=x,NC=(6-x),
由相似三角形的性质,得
MN:8=x:6,
解得MN=
| 4 |
| 3 |
由勾股定理,得
MC2=
| 25 |
| 9 |
MC′2=MC=
| 25 |
| 9 |
NC′2=
| 25 |
| 9 |
| 32 |
| 3 |
由勾股定理,得BC′2-BN2=C′N2,
即62-x2=
| 25 |
| 9 |
| 32 |
| 3 |
解得:x=6,
所以CM+NM=C′N=
| 15 |
| 2 |
故答案为:
| 15 |
| 2 |
点评:此题主要考查了利用轴对称求最短路线以及锐角三角函数关系应用,利用轴对称得出M点位置是解题关键.

练习册系列答案
相关题目
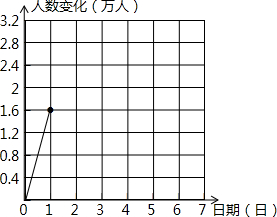 “十•一”黄金周期间,某风景区在7天假期中每天旅游的人数变化如下表(正数表示比前一天多的人数,负数表示比前一天少的人数)
“十•一”黄金周期间,某风景区在7天假期中每天旅游的人数变化如下表(正数表示比前一天多的人数,负数表示比前一天少的人数) 如图,点D、E在△ABC的边BC上的延长线上,且AB=BC=CD=DE,∠B=90°,则∠1+∠2+∠3=
如图,点D、E在△ABC的边BC上的延长线上,且AB=BC=CD=DE,∠B=90°,则∠1+∠2+∠3=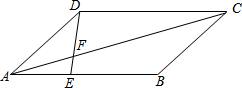 已知如图:?ABCD中,AE:EB=1:2,S△AEF=6cm2
已知如图:?ABCD中,AE:EB=1:2,S△AEF=6cm2