题目内容
抛物线y=x2+2x+3与x轴交点个数为 ．
考点：抛物线与x轴的交点
专题：
分析：先令x2+2x+3=0，求出△的值即可得出结论．
解答：解：令x2+2x+3=0，
∵△=22-4×1×3=-8＜0，
∴抛物线y=x2+2x+3与x轴没有交点．
故答案为：0．
∵△=22-4×1×3=-8＜0，
∴抛物线y=x2+2x+3与x轴没有交点．
故答案为：0．
点评：本题考查的是抛物线与x轴的交点问题，熟知二次函数y=ax2+bx+c（a，b，c是常数，a≠0）的交点与一元二次方程ax2+bx+c=0根之间的关系是解答此题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
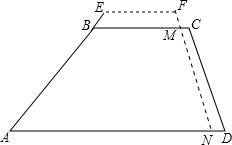如图，一个防汛坝的横断面是梯形ABCD，坝顶BC的宽为10米，坝高为5米，斜坡AB的坡比i1=1：1.5，斜坡CD的坡比i2=1：0.8．一次由于上游突降大雨，造成河水迅速上涨，为了及时加高坝身，只能用坝身后一侧CD处的土临时加高，现决定将CD一侧宽1米的土方全部用来加高坝身，且使坝身两侧的坡度与原来保持一致．问这样能使坝高增加多少米？（精确到0.1米）
如图是由几个完全相同的小立方块所堆成几何体俯视图，小正方形里的数字表示该位置小立方块的个数，请画出这个几何体的主视图和左视图．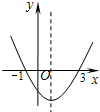
如图，为二次函数y=ax2+bx+c的图象，给出下列说法：①ab＜0；②方程ax2+bx+c=0的根为x1=-1，x2=3；③a+b+c＞0；④当x＞1时，y随x值的增大而增大；⑤当y＞0时，-1＜x＜3；⑥2a+b＜0．其中，正确的说法有
如图，在△ABC中，如果DE∥BC，AD=3，BD=4，则