题目内容
 如图,点D、E在△ABC的边BC上的延长线上,且AB=BC=CD=DE,∠B=90°,则∠1+∠2+∠3=
如图,点D、E在△ABC的边BC上的延长线上,且AB=BC=CD=DE,∠B=90°,则∠1+∠2+∠3=考点:相似三角形的判定与性质,勾股定理
专题:
分析:设AB=BC=CD=DE=x,利用勾股定理可求得AC=
x,AD=
x,AE=
x,CE=2x,从而证得△ACD∽△EAC,可得∠CAD=∠3,利用三角形外角性质可得∠1=∠2+∠3,且∠1=45°,可得出答案.
| 2 |
| 5 |
| 10 |
解答:解:设AB=BC=CD=DE=x,利用勾股定理可求得AC=
x,AD=
x,AE=
x,且CE=2x
∴
=
=
,
=
=
,
=
=
,
∴
=
=
,
∴△ACD∽△EAC,
∴∠CAD=∠3,
∴∠1=∠2+∠CAD=∠2+∠3,
∵AB=AC,∠ABC=90°,
∴∠1=45°,
∴∠1+∠2+∠3=2∠1=90°,
故答案为:90°.
| 2 |
| 5 |
| 10 |
∴
| CD |
| AC |
| x | ||
|
| ||
| 2 |
| AC |
| CE |
| ||
| 2x |
| ||
| 2 |
| AD |
| AE |
| ||
|
| ||
| 2 |
∴
| CD |
| AC |
| AC |
| CE |
| AD |
| AE |
∴△ACD∽△EAC,
∴∠CAD=∠3,
∴∠1=∠2+∠CAD=∠2+∠3,
∵AB=AC,∠ABC=90°,
∴∠1=45°,
∴∠1+∠2+∠3=2∠1=90°,
故答案为:90°.
点评:本题主要考查三角形相似的判定和性质,由条件证明△ACD∽△EAC是解题的关键.

练习册系列答案
相关题目
以下列各组线段为边,能组成三角形的是( )
| A、2cm,3cm,5cm |
| B、3cm,3cm,6cm |
| C、5cm,8cm,2cm |
| D、4cm,5cm,6cm |
 如图是由五块积木搭成,这几块积木都是相同的正方体,请画出从正面、左面、上面观察这个几何体你看到的图形.
如图是由五块积木搭成,这几块积木都是相同的正方体,请画出从正面、左面、上面观察这个几何体你看到的图形.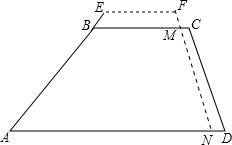 如图,一个防汛坝的横断面是梯形ABCD,坝顶BC的宽为10米,坝高为5米,斜坡AB的坡比i1=1:1.5,斜坡CD的坡比i2=1:0.8.一次由于上游突降大雨,造成河水迅速上涨,为了及时加高坝身,只能用坝身后一侧CD处的土临时加高,现决定将CD一侧宽1米的土方全部用来加高坝身,且使坝身两侧的坡度与原来保持一致.问这样能使坝高增加多少米?(精确到0.1米)
如图,一个防汛坝的横断面是梯形ABCD,坝顶BC的宽为10米,坝高为5米,斜坡AB的坡比i1=1:1.5,斜坡CD的坡比i2=1:0.8.一次由于上游突降大雨,造成河水迅速上涨,为了及时加高坝身,只能用坝身后一侧CD处的土临时加高,现决定将CD一侧宽1米的土方全部用来加高坝身,且使坝身两侧的坡度与原来保持一致.问这样能使坝高增加多少米?(精确到0.1米)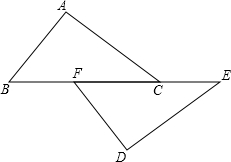 如图,点B、F、C、E在一条直线上,BC=EF,AB∥ED,AC∥FD,求证:AC=DF.
如图,点B、F、C、E在一条直线上,BC=EF,AB∥ED,AC∥FD,求证:AC=DF. 如图是由几个完全相同的小立方块所堆成几何体俯视图,小正方形里的数字表示该位置小立方块的个数,请画出这个几何体的主视图和左视图.
如图是由几个完全相同的小立方块所堆成几何体俯视图,小正方形里的数字表示该位置小立方块的个数,请画出这个几何体的主视图和左视图. 如图,在△ABC中,如果DE∥BC,AD=3,BD=4,则
如图,在△ABC中,如果DE∥BC,AD=3,BD=4,则