题目内容
7.(1)计算:$\frac{1}{1×3}$+$\frac{1}{2×4}$+$\frac{1}{3×5}$+…+$\frac{1}{9×11}$;(2)证明:对任意大于1的正整数n,有$\frac{1}{2×3}$+$\frac{1}{3×4}$+…+$\frac{1}{n(n+1)}$<$\frac{1}{2}$.
分析 (1)观察分析可知:$\frac{1}{1×3}=\frac{1}{2}×(1-\frac{1}{3})$,$\frac{1}{2×4}=\frac{1}{2}×(\frac{1}{2}-\frac{1}{4})$,$\frac{1}{3×5}=\frac{1}{2}×(\frac{1}{3}-\frac{1}{5})$,…,$\frac{1}{9×11}=\frac{1}{2}×(\frac{1}{9}-\frac{1}{11})$计算即可得出结论;
(2)观察分析可知:$\frac{1}{2×3}=\frac{1}{2}-\frac{1}{3}$,$\frac{1}{3×4}=\frac{1}{3}-\frac{1}{4}$,…,$\frac{1}{n(n+1)}=\frac{1}{n}-\frac{1}{n+1}$,据此规律可证得结论.
解答 (1)解:原式=$\frac{1}{2}×(1-\frac{1}{3})+\frac{1}{2}×(\frac{1}{2}-\frac{1}{4})+\frac{1}{2}×(\frac{1}{3}-\frac{1}{5})+…+\frac{1}{2}×(\frac{1}{9}-\frac{1}{11})$
=$\frac{1}{2}×(1-\frac{1}{3}+\frac{1}{2}-\frac{1}{4}+\frac{1}{3}-\frac{1}{5}+…+\frac{1}{9}-\frac{1}{11})$
=$\frac{1}{2}×(1+\frac{1}{2}-\frac{1}{10}-\frac{1}{11})$
=$\frac{1}{2}×\frac{72}{55}$
=$\frac{36}{55}$;
(2)证明:∵$\frac{1}{2×3}=\frac{1}{2}-\frac{1}{3}$,$\frac{1}{3×4}=\frac{1}{3}-\frac{1}{4}$,…,$\frac{1}{n(n+1)}=\frac{1}{n}-\frac{1}{n+1}$
∴$\frac{1}{2×3}+\frac{1}{3×4}+…+\frac{1}{n(n+1)}$
=$\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+…+\frac{1}{n}-\frac{1}{n+1}$
=$\frac{1}{2}-\frac{1}{n+1}$$<\frac{1}{2}$
∴$\frac{1}{2×3}+\frac{1}{3×4}+…+\frac{1}{n(n+1)}$$<\frac{1}{2}$.
点评 本题主要考查的是规律性问题,首先根据所给数据发现规律,再按规律逐步解答可完成.解题的关键是发现规律.

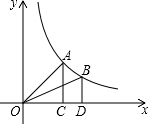 如图,过反比例函数y=$\frac{1}{x}$(x>0)的图象上任意两点A、B分别作x轴的垂线,垂足分别为C、D,连接OA、OB,设△AOC和△BOD的面积分别是S1、S2,比较它们的大小,可得( )
如图,过反比例函数y=$\frac{1}{x}$(x>0)的图象上任意两点A、B分别作x轴的垂线,垂足分别为C、D,连接OA、OB,设△AOC和△BOD的面积分别是S1、S2,比较它们的大小,可得( )| A. | S1>S2 | B. | S1=S2 | ||
| C. | S1>S2 | D. | 大小关系不能确定 |
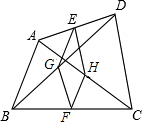 如图,在四边形ABCD中,AB=DC,E、F分别是AD、BC的中点,G、H分别是对角线BD、AC的中点.
如图,在四边形ABCD中,AB=DC,E、F分别是AD、BC的中点,G、H分别是对角线BD、AC的中点.