题目内容
7.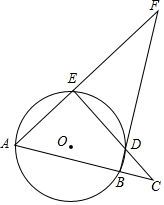 如图,分别延长圆内接四边形ABDE的两组对边,延长线相交于点F、C,若∠F=27°,∠A=53°,则∠C的度数为( )
如图,分别延长圆内接四边形ABDE的两组对边,延长线相交于点F、C,若∠F=27°,∠A=53°,则∠C的度数为( )| A. | 30° | B. | 43° | C. | 47° | D. | 53° |
分析 先根据三角形外角性质∠CBD=∠A+∠F=80°,根据圆内接四边形的性质得到∠A+∠BDE=180°,求得∠BDE=180°-53°=127°,根据三角形的外角的性质即可得到结论.
解答 解:∵∠A=53°,∠F=27°,
∴∠CBD=∠A+∠F=80°,
∵∠A+∠BDE=180°,
∴∠BDE=180°-53°=127°,
∵∠BDE=∠C+∠CBD,
∴∠C=127°-80°=47°.
故选C.
点评 本题考查了圆内接四边形的性质:圆内接四边形的对角互补;圆内接四边形的任意一个外角等于它的内对角.也考查了三角形外角性质.

练习册系列答案
相关题目
18.在实数0、π、$\frac{22}{7}$、$\sqrt{3}$、-$\sqrt{9}$中,无理数的个数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
2.当x=-6,y=$\frac{1}{6}$时,x2016y2017的值为( )
| A. | -6 | B. | 6 | C. | $-\frac{1}{6}$ | D. | $\frac{1}{6}$ |
12.已知直线y=ax+b(a≠0)经过点A(-3,0)和点B(0,2),那么关于x的方程ax+b=0的解是( )
| A. | x=-3 | B. | x=-1 | C. | x=0 | D. | x=2 |
16.下列计算正确的是( )
| A. | 2a-a=2 | B. | a2+a=a3 | C. | (x-1)2=x2-1 | D. | (a2)3=a6 |
17.下列事件中,为必然事件的是( )
| A. | 购买一张彩票,中奖 | |
| B. | 在标准状况下,加热到100℃时,水沸腾 | |
| C. | 任意画一个三角形,其内角和是360° | |
| D. | 射击运动员射击一次,命中靶心 |
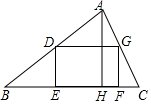 如图,四边形DEFG是△ABC的内接矩形,其中D、G分别在边AB,AC上,点E、F在边BC上,DG=2DE,AH是△ABC的高,BC=20,AH=15,那么矩形DEFG的周长是36.
如图,四边形DEFG是△ABC的内接矩形,其中D、G分别在边AB,AC上,点E、F在边BC上,DG=2DE,AH是△ABC的高,BC=20,AH=15,那么矩形DEFG的周长是36.