题目内容
19.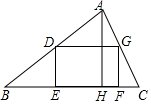 如图,四边形DEFG是△ABC的内接矩形,其中D、G分别在边AB,AC上,点E、F在边BC上,DG=2DE,AH是△ABC的高,BC=20,AH=15,那么矩形DEFG的周长是36.
如图,四边形DEFG是△ABC的内接矩形,其中D、G分别在边AB,AC上,点E、F在边BC上,DG=2DE,AH是△ABC的高,BC=20,AH=15,那么矩形DEFG的周长是36.
分析 根据相似三角形的判定和性质结论得到结论.
解答 解:∵DG∥BC,AH⊥BC,
∴AH⊥DG,△ADG∽△ABC,
∴$\frac{DG}{BC}=\frac{AH-DE}{AH}$,即$\frac{2DE}{20}=\frac{15-DE}{15}$,
∴DE=6,
∴DG=2DE=12,
∴矩形DEFG的周长=2×(6+12)=36.
故答案为:36.
点评 本题考查了相似三角形的判定和性质,矩形的性质,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.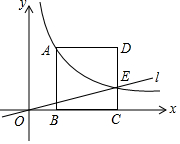 如图所示,正方形ABCD的顶点B,C在x轴的正半轴上,反比例函数y=$\frac{k}{x}$(k≠0)在第一象限的图象经过顶点A(m,m+3)和CD上的点E,且OB-CE=1.直线l过O、E两点,则tan∠EOC的值为( )
如图所示,正方形ABCD的顶点B,C在x轴的正半轴上,反比例函数y=$\frac{k}{x}$(k≠0)在第一象限的图象经过顶点A(m,m+3)和CD上的点E,且OB-CE=1.直线l过O、E两点,则tan∠EOC的值为( )
 如图所示,正方形ABCD的顶点B,C在x轴的正半轴上,反比例函数y=$\frac{k}{x}$(k≠0)在第一象限的图象经过顶点A(m,m+3)和CD上的点E,且OB-CE=1.直线l过O、E两点,则tan∠EOC的值为( )
如图所示,正方形ABCD的顶点B,C在x轴的正半轴上,反比例函数y=$\frac{k}{x}$(k≠0)在第一象限的图象经过顶点A(m,m+3)和CD上的点E,且OB-CE=1.直线l过O、E两点,则tan∠EOC的值为( )| A. | $\frac{9}{2}$ | B. | 5 | C. | $\frac{2}{9}$ | D. | 3 |
7.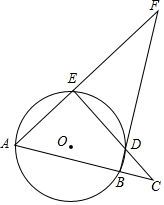 如图,分别延长圆内接四边形ABDE的两组对边,延长线相交于点F、C,若∠F=27°,∠A=53°,则∠C的度数为( )
如图,分别延长圆内接四边形ABDE的两组对边,延长线相交于点F、C,若∠F=27°,∠A=53°,则∠C的度数为( )
 如图,分别延长圆内接四边形ABDE的两组对边,延长线相交于点F、C,若∠F=27°,∠A=53°,则∠C的度数为( )
如图,分别延长圆内接四边形ABDE的两组对边,延长线相交于点F、C,若∠F=27°,∠A=53°,则∠C的度数为( )| A. | 30° | B. | 43° | C. | 47° | D. | 53° |
9.m是常数,若不等式组$\left\{\begin{array}{l}{x<1}\\{x>m-1}\end{array}\right.$恰有两个整数解,则m满足( )
| A. | m<-2 | B. | m=-2 | C. | m<-1 | D. | -1≤m<0 |
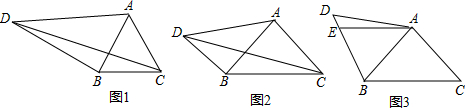
 如图,矩形ABCD的对角线相交于点O,∠AOB=60°,AB=4,则AC的长为8.
如图,矩形ABCD的对角线相交于点O,∠AOB=60°,AB=4,则AC的长为8.