题目内容
19.某校组织七年级师生进行秋游,学饺联系旅游公司提供车辆,该公司现有50座与35座两种车型,如果用35座的车,会有5人没座;如果全郁换乘50座的车,则可少用2辆车,而且多出15个座位.(1)问该校一共有多少名师生参加了这次活动?
(2)若35座车的日租金为250元/辆,50座车的日租金为320元/辆,在几种租车方案中,有哪种方案能使得座位刚好?用这种方案学校要出多少日租金?
分析 (1)设参加互动师生共x人,那么如果用35座的需$\frac{x-5}{35}$辆,全部换乘50座的需$\frac{x+15}{50}$辆,已知:如果全部换乘50座的,则可比35座车少用2辆,以此为等量关系列出方程求解;
(2)看什么时候所用租金最少,就选择该方案.
解答 解:(1)设参加互动师生共x人,
由题意得:$\frac{x-5}{35}=\frac{x+15}{50}$+2
即:10x-7x=105+50+700
解得:x=285人,
所以,参与本次师生互动的人共有285人.
(2)假设租了35座汽车x辆,其余人乘坐50座客车,则所花租金等于:
(285-35x)÷50×300+250x=(285-35x)6+250x=1710+40x,
若要使租金最少,即要使(1710+40x)值最小,
∴当x=1时,租金为1750元时为最低.
故租了35座汽车1辆,50座客车5辆最合算.
点评 本题主要考查一元一次方程的应用,(1)关键在于理解清楚题意,找出等量关系,列出方程求解;(2)运用“分类讨论”的方法,得出租金最少时的方案.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
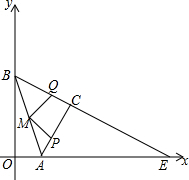 平面直角坐标系xOy中,已知A(1,0)、B(0,3).以AB为斜边作等腰直角三角形ABC,点C在第一象限,M是AB的中点.P、Q分别是线段AC、CB上的动点,点P自A出发,以$\frac{{\sqrt{5}}}{5}$个单位/s的速度向C运动;点Q自C出发,以相同速度向B运动.BC交x轴于点E.设运动时间为t s.
平面直角坐标系xOy中,已知A(1,0)、B(0,3).以AB为斜边作等腰直角三角形ABC,点C在第一象限,M是AB的中点.P、Q分别是线段AC、CB上的动点,点P自A出发,以$\frac{{\sqrt{5}}}{5}$个单位/s的速度向C运动;点Q自C出发,以相同速度向B运动.BC交x轴于点E.设运动时间为t s.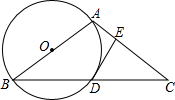 如图,AB是⊙O的直径,C是弦BD的延长线上一点,且BD=CD,连接AC,过点D作DE⊥AC,垂足为E.
如图,AB是⊙O的直径,C是弦BD的延长线上一点,且BD=CD,连接AC,过点D作DE⊥AC,垂足为E.