题目内容
2.直线y=-$\frac{3}{4}$x+3与x轴、y轴分别交于A、B两点,已知点C(0,-1)、D(0,k),以点D为圆心、DC为半径作⊙D,当⊙D与直线AB相切时,k的值为$\frac{7}{9}$.分析 根据题意可将A,B代入解析式中求出两点坐标;当圆与直线相切时,根据直线1与x轴的角度可求出圆心坐标,即可得出k的值.
解答 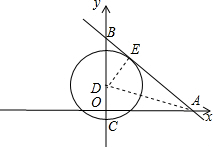 解:如图所示:
解:如图所示:
在y=-$\frac{3}{4}$x+3 中,令x=0,得y=3;令y=0,
得x=4,
故A,B两点的坐标分别为A(4,0),B(0,3).
若动圆的圆心在E处时与直线l相切,设切点为E,
如图所示,连接ED,则ED⊥AB.
可知$\left\{\begin{array}{l}{A{D}^{2}-D{E}^{2}=A{E}^{2}}\\{AE=AB-BE}\\{B{E}^{2}=B{D}^{2}-D{E}^{2}}\end{array}\right.$
代入数据得
k=$\frac{7}{9}$
故答案为:$\frac{7}{9}$.
点评 本题主要考查切线的性质,一次函数的应用,勾股定理,正确的作出图形是解题的关键.

练习册系列答案
相关题目
14.方程(x+2)2=4的根是( )
| A. | x1=4,x2=-4 | B. | x1=0,x2=-4 | C. | x1=0,x2=2 | D. | x1=0,x2=4 |
12. 如图,l1∥l2∥l3,AB=3,BC=2,EF=3,则DF的长为( )
如图,l1∥l2∥l3,AB=3,BC=2,EF=3,则DF的长为( )
 如图,l1∥l2∥l3,AB=3,BC=2,EF=3,则DF的长为( )
如图,l1∥l2∥l3,AB=3,BC=2,EF=3,则DF的长为( )| A. | 3 | B. | 5.5 | C. | 6.5 | D. | 7.5 |
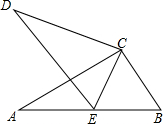 如图,将Rt△ABC绕直角顶点C顺时针旋转一定的角度到△DEC的位置,若E点在AB边上,且∠DCB=160°,则∠AED=70°.
如图,将Rt△ABC绕直角顶点C顺时针旋转一定的角度到△DEC的位置,若E点在AB边上,且∠DCB=160°,则∠AED=70°.
 请将下面的同类项用连线连接起来:
请将下面的同类项用连线连接起来: