题目内容
5. 已知:如图,Rt△ABC中,∠A=90°,BD平分∠ABC,CD⊥BD,垂足为D,DE⊥BC,垂足为E,试猜想DE与AC的长度关系,并加以证明.
已知:如图,Rt△ABC中,∠A=90°,BD平分∠ABC,CD⊥BD,垂足为D,DE⊥BC,垂足为E,试猜想DE与AC的长度关系,并加以证明.
分析 延长CD交BA的延长线于F,过D作DM⊥AF于M,由BD平分∠ABC,CD⊥BD,得到∠ABD=∠CBD,∠BDC=∠BDF=90°,推出△BDF≌△BDC,得到CD=DF,根据三角形中位线的性质得到DM=$\frac{1}{2}$AC,由角平分线的性质得到DE=DM,于是得到结论.
解答  解:延长CD交BA的延长线于F,过D作DM⊥AF于M,
解:延长CD交BA的延长线于F,过D作DM⊥AF于M,
∵BD平分∠ABC,CD⊥BD,
∴∠ABD=∠CBD,∠BDC=∠BDF=90°,
在△BDF与△CDB中,
$\left\{\begin{array}{l}{∠ABD=∠CBD}\\{BD=BD}\\{∠BDF=∠BDC}\end{array}\right.$,
∴△BDF≌△BDC,
∴CD=DF,
∵∠A=90°,
∴DM∥AC,
∴DM=$\frac{1}{2}$AC,
∵DE⊥BC,
∴DE=DM,
∴DE=$\frac{1}{2}$AC.
点评 本题考查了三角形的中位线的性质,全等三角形的判定和性质,三角形角平分线的性质,正确的作出辅助线是解题的关键.

练习册系列答案
相关题目
14.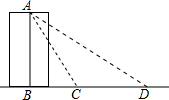 如图,要测量底部不能到达的一座塔的高度AB,甲、乙两名同学分别在C,D两处进行了测量.已知点B,C,D在同一直线上,且AB⊥BD,CD=12米,∠ACB=60°,∠ADB=30°,则塔的高度AB为( )
如图,要测量底部不能到达的一座塔的高度AB,甲、乙两名同学分别在C,D两处进行了测量.已知点B,C,D在同一直线上,且AB⊥BD,CD=12米,∠ACB=60°,∠ADB=30°,则塔的高度AB为( )
 如图,要测量底部不能到达的一座塔的高度AB,甲、乙两名同学分别在C,D两处进行了测量.已知点B,C,D在同一直线上,且AB⊥BD,CD=12米,∠ACB=60°,∠ADB=30°,则塔的高度AB为( )
如图,要测量底部不能到达的一座塔的高度AB,甲、乙两名同学分别在C,D两处进行了测量.已知点B,C,D在同一直线上,且AB⊥BD,CD=12米,∠ACB=60°,∠ADB=30°,则塔的高度AB为( )| A. | 12$\sqrt{3}$米 | B. | 6$\sqrt{3}$米 | C. | 12米 | D. | 6米 |