Question

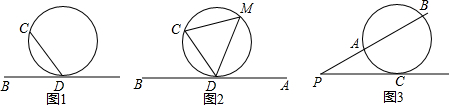
20．定义：由圆的切线和过切点的弦所组成的角叫做弦切角．如图1，已知AB切⊙O于D点，CD是⊙O的弦，
则图中∠BCD与∠ADC都是弦切角．
（1）如图2，作出∠BCD所夹弧CD所对的圆周角∠M，求证：∠BCD=∠M；
（2）请用文字语言总结（1）中的结论圆的一个弦切角等于它所夹弧所对的圆周角；
（3）如图3，PB切⊙O于B点，PAB交○O于A、B两点，利用（2）中结论，求证：PC²=PA•PB．

Answer 1

分析 （1）过D点作直径DE，连接CE，根据切线的性质和圆周角定理得出∠BCD+∠CDE=∠CDE+∠E=90°，求出∠BCD=∠E即可；
（2）根据（1）的结论得出即可；
（3）证△PAC∽△PCB，得出比例式，即可求出答案．

解答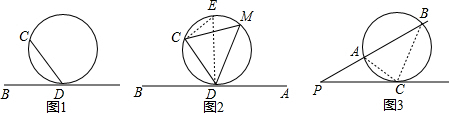
（1）证明：过D点作直径DE，连接CE，
∵DE是直径，BA切○O于D，
∴∠BCD+∠CDE=∠CDE+∠E=90°，
∴∠BCD=∠E，
又∵∠M=∠E，
∴∠BCD=∠M；

解：（2）结论：圆的一个弦切角等于它所夹弧所对的圆周角，
故答案为：圆的一个弦切角等于它所夹弧所对的圆周角；

（3）证明：连接AC、BC，由（2）知∠PCA=∠B，
又∵∠APC=∠CPB，
∴△PAC∽△PCB，
∴PA：PC=PC：PB，
即PC²=PA•PB．

点评 本题考查了圆周角定理，切线的性质，相似三角形的性质和判定的应用，能求出圆的一个弦切角等于它所夹弧所对的圆周角是解此题的关键．