题目内容
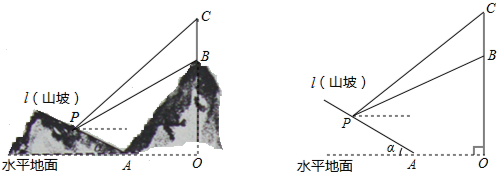
1. 如图,以⊙O上任意一点A为圆心,AO为半径画弧,与⊙O相交于B、C两点,点P为优弧BmC上任意一点,则∠P的度数是60°.
如图,以⊙O上任意一点A为圆心,AO为半径画弧,与⊙O相交于B、C两点,点P为优弧BmC上任意一点,则∠P的度数是60°.
分析 连结OB、AB、AO、OC、AC,如图,先判断△OAB和△OAC都是等边三角形,得到∠AOB=∠AOC=60°,然后根据圆周角定理求解.
解答  解:连结OB、AB、AO、OC、AC,如图,
解:连结OB、AB、AO、OC、AC,如图,
∵OA=OB=OC=AB=AC,
∴△OAB和△OAC都是等边三角形,
∴∠AOB=∠AOC=60°,
∴∠BOC=120°,
∴∠P=$\frac{1}{2}$∠BOC=60°.
故答案为60°.
点评 本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.也考查了等边三角形的判定与性质.

练习册系列答案
相关题目
12. 如图是一个正方体的表面展开图,如果相对面上所标的两个数互为相反数,那么图中x的值是( )
如图是一个正方体的表面展开图,如果相对面上所标的两个数互为相反数,那么图中x的值是( )
 如图是一个正方体的表面展开图,如果相对面上所标的两个数互为相反数,那么图中x的值是( )
如图是一个正方体的表面展开图,如果相对面上所标的两个数互为相反数,那么图中x的值是( )| A. | 8 | B. | 3 | C. | 2 | D. | -3 |
16.某课外小组的同学们在社会实践活动中调查了20个小区的入住率,得到的数据如下表:
则这些数据中的众数和中位数分别是( )
| 入住率 | 0.98 | 0.86 | 0.56 | 0.42 | 0.34 |
| 小区数 | 2 | 4 | 4 | 8 | 2 |
| A. | 0.56,0.34 | B. | 0.34,0.42 | C. | 0.42,0.49 | D. | 0.42,0.56 |
13.已知a>b,则下列不等式关系中正确的是( )
| A. | ac>bc | B. | ac2>bc2 | C. | a-1>b+1 | D. | a+1>b-1 |
11.据了解,H7N9禽流感病毒的直径大约是0.00 000 008米,则0.00 000 008用科学记数法表示为( )
| A. | 0.8×107 | B. | 8×10-8 | C. | 8×10-7 | D. | 8×10-6 |