题目内容
11．
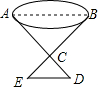如图，要测量一池塘两端AB的距离，可先在平地上取一个可以直接到达A和B的点C，连接AC并延长至D，使CD=$\frac{1}{5}$CA，连接BC，并延长至E，使CE=$\frac{1}{5}$CB，连接ED，如果量出DE=25m，那么池塘宽AB等于多少？
分析 利用相似三角形的判定方法得出△ACB∽△DCE，进而利用相似三角形的性质得出AB的长．
解答 解：∵CD=$\frac{1}{5}$CA，CE=$\frac{1}{5}$CB，且∠ACB=∠ECD，
∴△ACB∽△DCE，
∴$\frac{ED}{AB}$=$\frac{1}{5}$，
则$\frac{25}{AB}$=$\frac{1}{5}$，
故AB=125，
答：池塘宽AB等于25m．
点评 此题主要考查了相似三角形的应用，根据题意得出△ACB∽△DCE是解题关键．
练习册系列答案
阅读快车系列答案
相关题目
12．
如图，⊙O中，PC切⊙O于点C，连PO交于⊙O点A、B，点F是⊙O上一点，连PF，CD⊥AB于点D，AD=2，CD=4，则PF：DF的值是（ ）
如图，⊙O中，PC切⊙O于点C，连PO交于⊙O点A、B，点F是⊙O上一点，连PF，CD⊥AB于点D，AD=2，CD=4，则PF：DF的值是（ ）| A． | 2 | B． | $\sqrt{5}$ | C． | 5：3 | D． | 4：3 |
如图，DB为半圆的直径，A为BD延长线上一点，AC切半圆于点E，BC⊥AC于点C，交半圆于点F，已知BD=2，设AD=x，CF=y，求y关于x的函数解析式．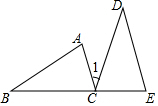
如图，B，C，E三点在同一直线上，AC∥DE，AC=CE=3cm，DE=5cm，∠1=∠B，则BE=8cm．
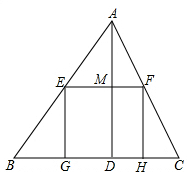△ABC是一块锐角三角形材料，边BC=120cm，高AD=80cm，要把它加工成矩形零件EFGH，使矩形的一边GH在BC上，其余两个顶点E、F在AB，AC上，
