题目内容
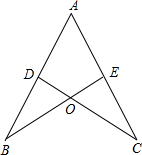 如图,AB=AC,CD⊥AB于D,BE⊥AC于E,BE与CD相交于点O.
如图,AB=AC,CD⊥AB于D,BE⊥AC于E,BE与CD相交于点O.(1)求证:AD=AE;
(2)连接OA,并证明OA平分∠DAE.
考点:全等三角形的判定与性质
专题:证明题
分析:(1)根据AAS推出△ACD≌△ABE,根据全等三角形的性质得出即可;
(2)证Rt△ADO≌Rt△AEO,即可得出∠DAO=∠EAO,即OA平分∠DAE.
(2)证Rt△ADO≌Rt△AEO,即可得出∠DAO=∠EAO,即OA平分∠DAE.
解答:证明:(1)∵CD⊥AB,BE⊥AC,
∴∠ADC=∠AEB=90°,
在△ACD和△ABE中,
,
∴△ACD≌△ABE(AAS),
∴AD=AE;
(2)证明: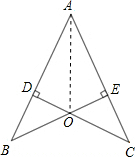 连接OA,
连接OA,
∵CD⊥AB,BE⊥AC,
∴∠ADC=∠AEB=90°.
在Rt△ADO和Rt△AEO中,
,
∴Rt△ADO≌Rt△AEO(HL).
∴∠DAO=∠EAO,
∴OA平分∠DAE.
∴∠ADC=∠AEB=90°,
在△ACD和△ABE中,
|
∴△ACD≌△ABE(AAS),
∴AD=AE;
(2)证明:
 连接OA,
连接OA,∵CD⊥AB,BE⊥AC,
∴∠ADC=∠AEB=90°.
在Rt△ADO和Rt△AEO中,
|
∴Rt△ADO≌Rt△AEO(HL).
∴∠DAO=∠EAO,
∴OA平分∠DAE.
点评:本题考查了全等三角形的判定方法,以及全等三角形的对应边相等,对应角相等的性质,难度适中.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
 在?ABCD中,若∠A=80°,则∠C等于( )
在?ABCD中,若∠A=80°,则∠C等于( )| A、10° | B、80° |
| C、100° | D、无法确定 |
 已知,如图:△ABC中,直线DF分别交BC、AD于D、E,交BA的延长线于点F,且
已知,如图:△ABC中,直线DF分别交BC、AD于D、E,交BA的延长线于点F,且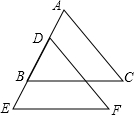 如图:AC∥DF,AD=BE,BC∥EF.求证:△ABC≌△DEF.
如图:AC∥DF,AD=BE,BC∥EF.求证:△ABC≌△DEF.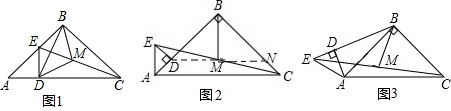
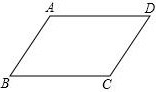 已知:如图,在四边形ABCD中,AB∥CD,∠B=∠D.求证:AD∥BC(用两种不同的方法证明)
已知:如图,在四边形ABCD中,AB∥CD,∠B=∠D.求证:AD∥BC(用两种不同的方法证明)