题目内容
7．先化简，再求值：$\frac{x}{x-y}$+$\frac{{y}^{3}}{x（x-y）^2}$÷$\frac{xy+{y}^{2}}{{y}^{2}-{x}^{2}}$，其中x=1，y=3．分析 先根据分式混合运算的法则把原式进行化简，再把x、y的值代入进行计算即可．
解答 解：原式=$\frac{x}{x-y}$+$\frac{{y}^{3}}{x（x-y）^{2}}$•$\frac{-（x+y）（x-y）}{y（x+y）}$
=$\frac{x}{x-y}$-$\frac{{y}^{2}}{x（x-y）}$
=$\frac{（x+y）（x-y）}{x（x-y）}$
=$\frac{x+y}{x}$，
当x=1，y=3时，原式=$\frac{1+3}{1}$=4．
点评 本题考查的是分式的化简求值，熟知分式混合运算的法则是解答此题的关键．
练习册系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
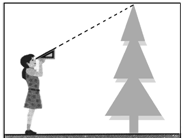小莉站在离一棵树水平距离为2米的地方，用一块含30°的直角三角板按如图所示的方式测量这棵树的高度，已知小莉的眼睛离地面的高度是1.5米，那么她测得这棵树的高度为（$\frac{2\sqrt{3}}{3}$+1.5）米．（结果保留根号）
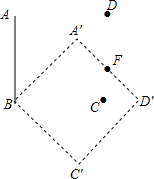如图所示，正方形ABCD的边长等于2，它绕顶点B按顺时针方向旋转得到正方形A′BC′D′．在这个旋转过程中：