题目内容
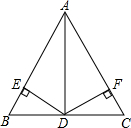 如图,在△ABC中,AB=5,AD=4,BD=DC=3,且DE⊥AB于点E,哪么DE=DF成立吗?试说明你的理由.
如图,在△ABC中,AB=5,AD=4,BD=DC=3,且DE⊥AB于点E,哪么DE=DF成立吗?试说明你的理由.考点:勾股定理的逆定理,角平分线的性质,等腰三角形的判定与性质
专题:
分析:先根据勾股定理的逆定理判断出△ABD的形状,故可得出△ABC是等腰三角形,由等腰三角形的性质可知AD是∠BAC的平分线,根据角平分线的性质即可得出结论.
解答:解:∵AB=5,AD=4,BD=3,52=32+42,
∴△ABD是直角三角形.
∵BD=DC=3,
∴AB=AC,即△ABC是等腰三角形.
∴AD是∠BAC的平分线,
∵DE⊥AB,DF⊥AC,
∴DE=DF.
∴△ABD是直角三角形.
∵BD=DC=3,
∴AB=AC,即△ABC是等腰三角形.
∴AD是∠BAC的平分线,
∵DE⊥AB,DF⊥AC,
∴DE=DF.
点评:本题考查的是勾股定理的逆定理,熟知如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形是解答此题的关键.

练习册系列答案
相关题目
下列图形中,既是轴对称图形又是中心对称图形的是( )
| A、等边三角形 | B、平行四边形 |
| C、菱形 | D、梯形 |
在Rt△ABC中,∠C=90゜,AC=5,BC=12,以C为圆心,R为半径作圆与斜边AB相切,则R的值为( )
A、
| ||
B、
| ||
C、
| ||
| D、5 |

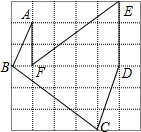 如图,这是由36个边长为1的小正方形拼成的方格图,依次连接小正方形的顶点A,B,C,D,E,F得线段AB,BC,CD,DE,EF,FA,请说出这些线段中的长度是有理数的有哪些,是无理数的有哪些,并在数轴上作出表示
如图,这是由36个边长为1的小正方形拼成的方格图,依次连接小正方形的顶点A,B,C,D,E,F得线段AB,BC,CD,DE,EF,FA,请说出这些线段中的长度是有理数的有哪些,是无理数的有哪些,并在数轴上作出表示