题目内容
如图,∠B、∠D的两边分别平行.
(1)在图①中,∠B与∠D的数量关系是什么?为什么?
(2)在图②中,∠B与∠D的数量关系是什么?为什么?
(3)由(1)(2)可得结论 ;
(4)应用:若两个角的两边两两互相平行,其中一个角比另一个角的2倍少30°,求这两个角的度数.

(1)在图①中,∠B与∠D的数量关系是什么?为什么?
(2)在图②中,∠B与∠D的数量关系是什么?为什么?
(3)由(1)(2)可得结论
(4)应用:若两个角的两边两两互相平行,其中一个角比另一个角的2倍少30°,求这两个角的度数.

考点:平行线的性质
专题:
分析:(1)由AB∥CD,BE∥DF,根据两直线平行,内错角相等,可得∠B=∠1,∠1=∠D,即可得∠B=∠D;
(2)由AB∥CD,BE∥DF,根据两直线平行,内错角相等,同旁内角互补,可得∠B=∠1,∠1+∠D=180°,即可得∠B+∠D=180°.
(3)由(1)(2)可得结论:若两个角的两边两两互相平行,则这两个角相等或互补;
(4)由两个角的两边两两互相平行,可得这两个角的相等或互补,即可求得答案.
(2)由AB∥CD,BE∥DF,根据两直线平行,内错角相等,同旁内角互补,可得∠B=∠1,∠1+∠D=180°,即可得∠B+∠D=180°.
(3)由(1)(2)可得结论:若两个角的两边两两互相平行,则这两个角相等或互补;
(4)由两个角的两边两两互相平行,可得这两个角的相等或互补,即可求得答案.
解答: 解:(1)∠B=∠D.
解:(1)∠B=∠D.
理由:∵AB∥CD,BE∥DF,
∴∠B=∠1,∠1=∠D,
∴∠B=∠D.
(2)∠B+∠D=180°,
理由:∵AB∥CD,BE∥DF,
∴∠B=∠1,∠1+∠D=180°,
∴∠B+∠D=180°.
(3)由(1)(2)可得结论:若两个角的两边两两互相平行,则这两个角相等或互补.
故答案为:若两个角的两边两两互相平行,则这两个角相等或互补.
(4)设一个角为x°,则另一个角的(2x-30)°,
若相等:x=2x-30,
解得:x=30,
则这两角分别为:30°,30°;
若互补,则x+2x-30=180,
解得:x=70,
则这两角分别为:70°,110°;
答:这两个角的度数分别为:30°,30°或70°,110°.
 解:(1)∠B=∠D.
解:(1)∠B=∠D.理由:∵AB∥CD,BE∥DF,
∴∠B=∠1,∠1=∠D,
∴∠B=∠D.
(2)∠B+∠D=180°,
理由:∵AB∥CD,BE∥DF,
∴∠B=∠1,∠1+∠D=180°,
∴∠B+∠D=180°.
(3)由(1)(2)可得结论:若两个角的两边两两互相平行,则这两个角相等或互补.
故答案为:若两个角的两边两两互相平行,则这两个角相等或互补.
(4)设一个角为x°,则另一个角的(2x-30)°,
若相等:x=2x-30,
解得:x=30,
则这两角分别为:30°,30°;
若互补,则x+2x-30=180,
解得:x=70,
则这两角分别为:70°,110°;
答:这两个角的度数分别为:30°,30°或70°,110°.
点评:此题考查了平行线的性质.此题难度适中,注意掌握数形结合思想与方程思想的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
三角形三边分别3cm,6cm,xcm,则x可能是( )
| A、1 | B、2 | C、3 | D、4 |
圆外一点P,PA、PB分别切⊙O于A、B,C为优弧AB上一点,若∠ACB=α,则∠APB=( )
| A、180°-α |
| B、90°-α |
| C、90°+α |
| D、180°-2α |
 如图,点A、B、C都在⊙O上,∠AOB=∠BOC=120°.求证:△ABC是等边三角形.
如图,点A、B、C都在⊙O上,∠AOB=∠BOC=120°.求证:△ABC是等边三角形.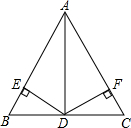 如图,在△ABC中,AB=5,AD=4,BD=DC=3,且DE⊥AB于点E,哪么DE=DF成立吗?试说明你的理由.
如图,在△ABC中,AB=5,AD=4,BD=DC=3,且DE⊥AB于点E,哪么DE=DF成立吗?试说明你的理由. 如图,正方形ABCD中,点E在边CD上,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF.
如图,正方形ABCD中,点E在边CD上,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF. 如图,E在AB上,F在DC上,G是BC延长线上的一点;
如图,E在AB上,F在DC上,G是BC延长线上的一点;