题目内容
已知M、N分别表示不同的单项式,且3x(M-5x)=6x2y3+N,求M、N.
考点:单项式乘多项式
专题:
分析:根据单项式与多项式相乘,先用单项式乘多项式的每一项,再把所得的积相加计算即可求出M,N的值.
解答:解:∵3x(M-5x)=6x2y3+N,
∴3xM-15x2=6x2y3+N,
∴M=2xy3,N=-15x2.
∴3xM-15x2=6x2y3+N,
∴M=2xy3,N=-15x2.
点评:此题考查了单项式与多项式相乘,熟练掌握运算法则是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
(x2+ax+8)(x2-3x+b)展开式中不含x3和x2项,则a、b的值分别为( )
| A、a=3,b=1 |
| B、a=-3,b=1 |
| C、a=0,b=0 |
| D、a=3,b=8 |
下列说法中,正确的是( )
| A、(-3)2是负数 |
| B、最小的有理数是0 |
| C、若|x|=5,则x=5或x=-5 |
| D、任何有理数的绝对值都大于0 |
已知关于x的方程ax-8=20+a的解是x=-3,则a的值为( )
| A、-4 | B、-6 | C、-7 | D、-3 |
从1、2、3、4中任取一个数作为十位上的数字,再从3、4、5中任取一个数作为个位上的数字,那么组成的两位数是3的倍数的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,点A、B、C都在⊙O上,∠AOB=∠BOC=120°.求证:△ABC是等边三角形.
如图,点A、B、C都在⊙O上,∠AOB=∠BOC=120°.求证:△ABC是等边三角形.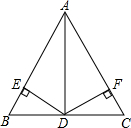 如图,在△ABC中,AB=5,AD=4,BD=DC=3,且DE⊥AB于点E,哪么DE=DF成立吗?试说明你的理由.
如图,在△ABC中,AB=5,AD=4,BD=DC=3,且DE⊥AB于点E,哪么DE=DF成立吗?试说明你的理由.