题目内容
在Rt△ABC中,∠C=90゜,AC=5,BC=12,以C为圆心,R为半径作圆与斜边AB相切,则R的值为( )
A、
| ||
B、
| ||
C、
| ||
| D、5 |
考点:切线的性质,勾股定理
专题:计算题
分析:作CD⊥AB于D,如图,先利用勾股定理计算出AB=13,再利用面积法计算出CD=
,然后根据切线的性质易得R=CD=
.
| 60 |
| 13 |
| 60 |
| 13 |
解答:解: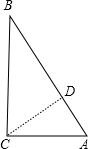 作CD⊥AB于D,如图,
作CD⊥AB于D,如图,
∵∠C=90゜,AC=5,BC=12,
∴AB=
=13,
∵
CD•AB=
CB•CA,
∴CD=
=
,
∵以C为圆心,R为半径作圆与斜边AB相切,
∴R=CD=
.
故选A.
 作CD⊥AB于D,如图,
作CD⊥AB于D,如图,∵∠C=90゜,AC=5,BC=12,
∴AB=
| AC2+BC2 |
∵
| 1 |
| 2 |
| 1 |
| 2 |
∴CD=
| 5×12 |
| 13 |
| 60 |
| 13 |
∵以C为圆心,R为半径作圆与斜边AB相切,
∴R=CD=
| 60 |
| 13 |
故选A.
点评:本题考查了切线的性质:圆的切线垂直于经过切点的半径.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.也考查了勾股定理.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列说法中,正确的是( )
| A、(-3)2是负数 |
| B、最小的有理数是0 |
| C、若|x|=5,则x=5或x=-5 |
| D、任何有理数的绝对值都大于0 |
圆外一点P,PA、PB分别切⊙O于A、B,C为优弧AB上一点,若∠ACB=α,则∠APB=( )
| A、180°-α |
| B、90°-α |
| C、90°+α |
| D、180°-2α |
从1、2、3、4中任取一个数作为十位上的数字,再从3、4、5中任取一个数作为个位上的数字,那么组成的两位数是3的倍数的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
小红家的冰箱冷藏室温度是3℃,冷冻室的温度是-1℃,则她家的冰箱冷藏室比冷冻室温度高( )
| A、4℃ | B、-4℃ |
| C、2℃ | D、-2℃ |
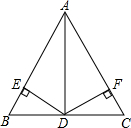 如图,在△ABC中,AB=5,AD=4,BD=DC=3,且DE⊥AB于点E,哪么DE=DF成立吗?试说明你的理由.
如图,在△ABC中,AB=5,AD=4,BD=DC=3,且DE⊥AB于点E,哪么DE=DF成立吗?试说明你的理由. 如图,正方形ABCD中,点E在边CD上,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF.
如图,正方形ABCD中,点E在边CD上,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF.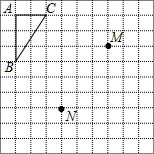 在方格纸中平移三角形ABC,使点A移到点M,点B和点C应移到什么位置?再将三角形ABC由点M平移到点N,分别画出两次平移后的三角形,如果直接平移ABC,使点A移到点N,它和我们前面得到的三角形位置相同吗?
在方格纸中平移三角形ABC,使点A移到点M,点B和点C应移到什么位置?再将三角形ABC由点M平移到点N,分别画出两次平移后的三角形,如果直接平移ABC,使点A移到点N,它和我们前面得到的三角形位置相同吗?