题目内容
16. (1)计算:(-3)2-$\sqrt{12}$+6cos30°+(tan60°-5)0;
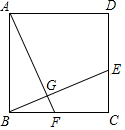
(1)计算:(-3)2-$\sqrt{12}$+6cos30°+(tan60°-5)0;(2)已知:在正方形ABCD中,线段AE、BF相交于点G,且BE=CF,求证:AE⊥BF.
分析 (1)根据幂的乘方法则、二次根式的化简法则、特殊角三角函数值、非零数的零次幂化简计算即可.
(2)只要证明△ABF≌△BCE,推出∠BAF=∠EBC,由∠EBC+∠ABE=90°,推出∠BAF+∠ABE=90°,推出∠AGB=90°.
解答 解:(1)原式=9-2$\sqrt{3}$+3$\sqrt{3}$+1=10+$\sqrt{3}$.
(2)证明: ∵四边形ABCD是正方形,
∵四边形ABCD是正方形,
∴AB=BC,∠ABF=∠C=90°,
在△ABF和△BCE中,
$\left\{\begin{array}{l}{AB=BC}\\{∠ABF=∠C}\\{BF=EC}\end{array}\right.$,
∴△ABF≌△BCE,
∴∠BAF=∠EBC,
∵∠EBC+∠ABE=90°,
∴∠BAF+∠ABE=90°,
∴∠AGB=90°,
∴AF⊥BE.
点评 本题考查幂的乘方法则、二次根式的化简法则、特殊角三角函数值、非零数的零次幂、正方形的性质、全等三角形的判定和性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6.用直尺和圆规作一个角等于已知角的示意图如下,则说明∠A′O′B′=∠AOB的依据是( )
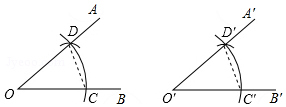
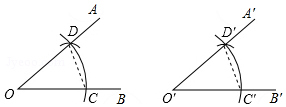
| A. | 边角边 | B. | 边边边 | C. | 角边角 | D. | 角角边 |
 画图并填空:如图,方格纸中每个小正方形的边长都为1.在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.利用网格点和三角板画图或计算:
画图并填空:如图,方格纸中每个小正方形的边长都为1.在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.利用网格点和三角板画图或计算: