题目内容
14．
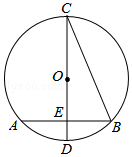如图，在⊙O中，CD是直径，弦AB⊥CD，垂足为E，连接BC，若AB=2$\sqrt{2}$cm，∠BCD=22°30′，则⊙O的半径为（ ）| A． | 4cm | B． | 3cm | C． | 2cm | D． | 1cm |
分析 连接BC、BO，根据∠BCD=22°30′可得∠BOD=45°，再根据垂径定理可得EB=$\sqrt{2}$cm，最后利用特殊角的三角函数可得答案．
解答 
解：连接BC、BO，
∵∠BCD=22°30′，
∴∠BOD=45°，
∵弦AB⊥CD，AB=2$\sqrt{2}$cm，
∴EB=$\sqrt{2}$cm，
∴BO=2cm．
故选C．
点评 此题主要考查了圆周角定理、垂径定理、以及三角函数的应用，关键是掌握圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．
练习册系列答案
提分百分百检测卷系列答案
宝贝计划期末冲刺夺100分系列答案
能考试全能100分系列答案
相关题目
已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，下列结论：
19．下列说法：
①射线AB和射线BA是同一条射线；
②若AB=BC，则点B为线段AC的中点；
③同角的补角相等；
④点C在线段AB上，M，N分别是线段AC，CB的中点．若MN=5，则线段AB=10．
其中说法正确的是（ ）
①射线AB和射线BA是同一条射线；
②若AB=BC，则点B为线段AC的中点；
③同角的补角相等；
④点C在线段AB上，M，N分别是线段AC，CB的中点．若MN=5，则线段AB=10．
其中说法正确的是（ ）
| A． | ①② | B． | ②③ | C． | ②④ | D． | ③④ |
6．
如图，一个三角板的直角顶点在直线l上，∠1=35°，那么∠2=（ ）
如图，一个三角板的直角顶点在直线l上，∠1=35°，那么∠2=（ ）| A． | 35° | B． | 65° | C． | 55° | D． | 90° |
3．设tan 69.83°=a，则tan 20.17°用a可表示为（ ）
| A． | -a | B． | $\frac{1}{a}$ | C． | $\frac{a}{3}$ | D． | $\sqrt{a}$ |
4．在△ABC中，∠C=90°，若∠A=30°，则sinA+cosB的值等于（ ）
| A． | 1 | B． | $\frac{1-\sqrt{3}}{2}$ | C． | $\frac{1+\sqrt{3}}{2}$ | D． | $\frac{1}{4}$ |