题目内容
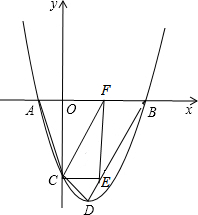 如图抛物线y=x2+bx+c(c<0)与x轴交于A、B两点,(点A在点B的左侧),与y轴交于点C,顶点为D,且OB=OC=3,点E为线段BD上的一个动点,EF⊥x轴于F.
如图抛物线y=x2+bx+c(c<0)与x轴交于A、B两点,(点A在点B的左侧),与y轴交于点C,顶点为D,且OB=OC=3,点E为线段BD上的一个动点,EF⊥x轴于F.(1)求抛物线的解析式;
(2)是否存在点E,使△ECF为直角三角形?若存在,求点E的坐标;不存在,请说明理由;
(3)连接AC、BC,若点P是抛物线上的一个动点,当P运动到什么位置时,∠PCB=∠ACO,请直接写出点P的坐标.
考点:二次函数综合题
专题:
分析:(1)易求得点B,C坐标,即可求得b、c的值,即可解题;
(2)易求得顶点D的坐标,即可求得直线BD的解析式,根据∠CEF=90°,即可求得点E纵坐标为-3,即可解题;
(3)存在2种情况:①∠PCB=∠ACO,②∠P'CB=∠ACO,可分别求得tan∠PCE的值,即可求得直线PC斜率,即可求得直线PC于抛物线交点P坐标,即可解题.
(2)易求得顶点D的坐标,即可求得直线BD的解析式,根据∠CEF=90°,即可求得点E纵坐标为-3,即可解题;
(3)存在2种情况:①∠PCB=∠ACO,②∠P'CB=∠ACO,可分别求得tan∠PCE的值,即可求得直线PC斜率,即可求得直线PC于抛物线交点P坐标,即可解题.
解答:解:(1)∵OB=OC=3,
∴点B坐标为(3,0),点C坐标为(0,-3),
∵抛物线y=x2+bx+c经过点B,C,∴
,
解得:c=-3,b=-2,
∴抛物线的解析式为y=x2-2x-3;
(2)∵抛物线的解析式为y=x2-2x-3,
∴点D坐标为(1,-4),
∵直线BD经过点B,D,设直线BD解析式为y=kx+b,
则
,
解得:k=2,b=-6,
∴直线BD解析式为y=2x-6,
∵△ECF为直角三角形,
∴∠CEF=90°,
∴点E纵坐标为-3,
∴点E横坐标为
,
∴点E坐标为(
,-3);
(3)存在2种情况:
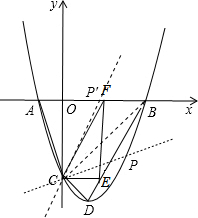
①∠PCB=∠ACO,
∵∠BCE=45°,
∴tan∠BCE=1,
∵tan∠ACO=
,
∴tan∠PCB=
,
∴tan∠PCE=tan(∠BCE-∠PCB)=
=
,
∵直线PC经过点P,
∴直线PC解析式为:y=
x-3,
∴点P坐标为:(
,-
),
②∠P'CB=∠ACO,
∵∠BCE=45°,
∴tan∠BCE=1,
∵tan∠ACO=
,
∴tan∠P'CB=
,
∴tan∠P'CE=tan(∠BCE-∠P'CB)=
=2,
∵直线PC经过点P,
∴直线PC解析式为:y=2x-3,
∴点P坐标为:(4,5).
∴点B坐标为(3,0),点C坐标为(0,-3),
∵抛物线y=x2+bx+c经过点B,C,∴
|
解得:c=-3,b=-2,
∴抛物线的解析式为y=x2-2x-3;
(2)∵抛物线的解析式为y=x2-2x-3,
∴点D坐标为(1,-4),
∵直线BD经过点B,D,设直线BD解析式为y=kx+b,
则
|
解得:k=2,b=-6,
∴直线BD解析式为y=2x-6,
∵△ECF为直角三角形,
∴∠CEF=90°,
∴点E纵坐标为-3,
∴点E横坐标为
| 3 |
| 2 |
∴点E坐标为(
| 3 |
| 2 |
(3)存在2种情况:

①∠PCB=∠ACO,
∵∠BCE=45°,
∴tan∠BCE=1,
∵tan∠ACO=
| 1 |
| 3 |
∴tan∠PCB=
| 1 |
| 3 |
∴tan∠PCE=tan(∠BCE-∠PCB)=
1-
| ||
1+
|
| 1 |
| 2 |
∵直线PC经过点P,
∴直线PC解析式为:y=
| 1 |
| 2 |
∴点P坐标为:(
| 5 |
| 2 |
| 7 |
| 4 |
②∠P'CB=∠ACO,
∵∠BCE=45°,
∴tan∠BCE=1,
∵tan∠ACO=
| 1 |
| 3 |
∴tan∠P'CB=
| 1 |
| 3 |
∴tan∠P'CE=tan(∠BCE-∠P'CB)=
1+
| ||
1-
|
∵直线PC经过点P,
∴直线PC解析式为:y=2x-3,
∴点P坐标为:(4,5).
点评:本题考查了二次函数顶点的求解,考查了二次函数解析式的求解,考查了直线和抛物线交点的求解,本题中求得抛物线解析式是解题的关键.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案
相关题目
 如图是一个梯形和圆.
如图是一个梯形和圆.