题目内容
 如图,AB是⊙O的直径,CD是切线,AC⊥CD,DE⊥AB,求证:DE2=AC•FC.
如图,AB是⊙O的直径,CD是切线,AC⊥CD,DE⊥AB,求证:DE2=AC•FC.考点:切线的性质,相似三角形的判定与性质
专题:证明题
分析:连接OD,BE,交于点G,则可知四边形CDGF为矩形,CD=FG=GB,可证明△OBG≌△ODE,可知DE=CD,结合切割线定理可得出结论.
解答: 证明:
证明:
连接OD,BE,交于点G,
∵CD是切线,
∴∠ODC=90°,
∵AB为直径,
∴∠CFB=90°,且AC⊥CD,
∴四边形CDGF为矩形,
∴CD=FG,OD∥AC,
∵O为AB中点,
∴G为BF中点,
∴BG=FG=CD,
在△OBG和△ODE中
∴△OBG≌△ODE(AAS),
∴CD=DE,
又CD为切线,AC为割线,
∴CD2=AC•CF,
∴DE2=AC•CF.
 证明:
证明:连接OD,BE,交于点G,
∵CD是切线,
∴∠ODC=90°,
∵AB为直径,
∴∠CFB=90°,且AC⊥CD,
∴四边形CDGF为矩形,
∴CD=FG,OD∥AC,
∵O为AB中点,
∴G为BF中点,
∴BG=FG=CD,
在△OBG和△ODE中
|
∴△OBG≌△ODE(AAS),
∴CD=DE,
又CD为切线,AC为割线,
∴CD2=AC•CF,
∴DE2=AC•CF.
点评:本题主要考查切线的性质及全等三角形的判定和性质,由条件证明CD=DE是解题的关键.注意切割线定理的应用.

练习册系列答案
相关题目
下列说法正确的是( )
| A、单项式-mn的次数是0 | ||||
B、单项式-
| ||||
C、单项式-
| ||||
| D、-5是一次单项式 |
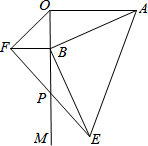 如图,AO⊥OM,OA=8
如图,AO⊥OM,OA=8| 2 |
| A、4 | ||
B、4
| ||
C、6
| ||
| D、BP的长度随B点的运动而变化 |
把抛物线y=-x2的图象向左平移2个单位,再向上平移3个单位,所得的抛物线的函数关系是( )
| A、y=-x2+2 |
| B、y=-x2+1 |
| C、y=-( x-2)2+1 |
| D、y=-( x+2)2+3 |
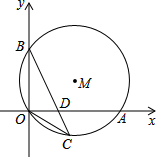 如图,⊙M经过O点,并且与x轴、y轴分别交与A、B两点,线段OA,OB(OA>OB)的长时方程x2-17x+60=0的两根.
如图,⊙M经过O点,并且与x轴、y轴分别交与A、B两点,线段OA,OB(OA>OB)的长时方程x2-17x+60=0的两根.
 如图:AC=DB,AB=DC,求证:∠A=∠D.
如图:AC=DB,AB=DC,求证:∠A=∠D.
