题目内容
已知点C是线段上一点,CD=
,AB=20,点E是线段AC中点.
(1)DE=4,则BC= ;若DE=m,则BC= ;DE与BC的数量关系是 ;
(2)当点D在直线AB上时,(1)中的DE与BC的数量关系是否成立?请说明理由;
(3)在(2)的条件下,若DE=7,在直线AB上是否存在一点M,使得BM与AC的一半的和等于CD与BM的差?若存在,请直接写出BM的长度;若不存在,请说明理由.
| AB |
| 2 |
(1)DE=4,则BC=
(2)当点D在直线AB上时,(1)中的DE与BC的数量关系是否成立?请说明理由;
(3)在(2)的条件下,若DE=7,在直线AB上是否存在一点M,使得BM与AC的一半的和等于CD与BM的差?若存在,请直接写出BM的长度;若不存在,请说明理由.
考点:两点间的距离
专题:
分析:(1)根据线段的和差,可得EC的长,根据线段中点的性质,可得AC的长,根据线段的和差,可得答案;
(2)根据线段的和差,可得EC的长,根据线段中点的性质,可得AC的长,根据线段的和差,可得答案;
(3)根据线段的和差,可得EC的长,根据线段中点的性质,可得AC的长,根据BM+
AC=CD+BM,可得方程,根据解方程,可得答案.
(2)根据线段的和差,可得EC的长,根据线段中点的性质,可得AC的长,根据线段的和差,可得答案;
(3)根据线段的和差,可得EC的长,根据线段中点的性质,可得AC的长,根据BM+
| 1 |
| 2 |
解答:解:如图:
 ,
,
(1)由CD=
,AB=20,得
CD=10.
由线段的和差,得
EC=DC-DE=10-4=6.
由E是点E是线段AC中点,得
AC=2AE=2CE=12.
由线段的和差,得
BC=AB-AC=20-12=8,
由CD=
,AB=20,得
CD=10.
由线段的和差,得
EC=DC-DE=10-m.
由E是点E是线段AC中点,得
AE=CE=m.
由线段的和差,得
BC=AB-AC=20-m-m=20-2m,
DE与BC的数量关系是BC=AB-2DE,
故答案为:8,320-2m,BC=AB-2DE;
(2)当点D在直线AB上时,(1)中的DE与BC的数量关系成立,理由如下:
如图: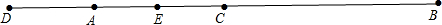 ,
,
由线段的和差,得
CE=10-DE.
由线段中点的性质,得
AC=2CE=20-2DE.
BC=AB-AC=20-(20-2DE)=2DE.
(3)存在,BM=3.5.
 ,
,(1)由CD=
| AB |
| 2 |
CD=10.
由线段的和差,得
EC=DC-DE=10-4=6.
由E是点E是线段AC中点,得
AC=2AE=2CE=12.
由线段的和差,得
BC=AB-AC=20-12=8,
由CD=
| AB |
| 2 |
CD=10.
由线段的和差,得
EC=DC-DE=10-m.
由E是点E是线段AC中点,得
AE=CE=m.
由线段的和差,得
BC=AB-AC=20-m-m=20-2m,
DE与BC的数量关系是BC=AB-2DE,
故答案为:8,320-2m,BC=AB-2DE;
(2)当点D在直线AB上时,(1)中的DE与BC的数量关系成立,理由如下:
如图:
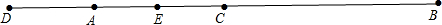 ,
,由线段的和差,得
CE=10-DE.
由线段中点的性质,得
AC=2CE=20-2DE.
BC=AB-AC=20-(20-2DE)=2DE.
(3)存在,BM=3.5.
点评:本题考查了两点间的距离,利用了线段的和差,线段中点的性质,解一元一次方程,运用知识点较多,题目稍有难度.

练习册系列答案
相关题目
下列不是有相反意义的量是( )
| A、上升5米与下降3米 |
| B、零下5℃与零下1℃ |
| C、高出海拔100米与低于海拔10米 |
| D、亏损100元与收入100元 |
在-
,
,
,0.3030030003,-
,3.14中,无理数的个数为( )
| π |
| 3 |
| 3 | 64 |
| 7 |
| 22 |
| 7 |
| A、2个 | B、3个 | C、4个 | D、5个 |
 如图,AB是⊙O的直径,CD是切线,AC⊥CD,DE⊥AB,求证:DE2=AC•FC.
如图,AB是⊙O的直径,CD是切线,AC⊥CD,DE⊥AB,求证:DE2=AC•FC.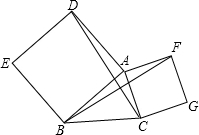 以△ABC的AB、AC为边分别作正方形ADEB、ACGF,连接DC、BF.
以△ABC的AB、AC为边分别作正方形ADEB、ACGF,连接DC、BF.