Question

如图，P₁（x₁，y₁），P₂（x₂，y₂），…P_n（x_n，y_n）在函数y=

1

x

（x＞0）的图象上，△P₁OA₁，△P₂A₁A₂，△P₃A₂A₃，…△P_nA_n-1A_n都是等腰直角三角形，斜边OA₁、A₁A₂、A₂A₃，…A_n-1A_n都在x轴上（n是大于或等于2的正整数），则点P₂₀₁₄的坐标是

 

．

Answer 1

考点：反比例函数图象上点的坐标特征,等腰直角三角形

专题：规律型

分析：过点P₁作P₁E⊥x轴于点E，过点P₂作P₂F⊥x轴于点F，过点P₃作P₃G⊥x轴于点G，根据△P₁OA₁，△P₂A₁A₂，△P₃A₂A₃都是等腰直角三角形，可求出P₁，P₂，P₃的坐标，从而总结出一般规律得出点P_n的坐标．

解答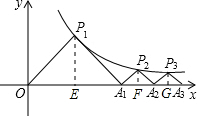：解：过点P₁作P₁E⊥x轴于点E，过点P₂作P₂F⊥x轴于点F，过点P₃作P₃G⊥x轴于点G，
∵△P₁OA₁是等腰直角三角形，
∴P₁E=OE=A₁E=OA₁，
设点P₁的坐标为（a，a），（a＞0），
将点P₁（a，a）代入y=

1

x

，可得a=1，
故点P₁的坐标为（1，1），
则OA₁=2a，
设点P₂的坐标为（b+2，b），将点P₂（b+2，b）代入y=

1

x

，可得b=

2

-1，
故点P₂的坐标为（

2

+1，

2

-1），
则A₁F=A₂F=

2

-1，OA₂=OA₁+A₁A₂=2

2

，
设点P₃的坐标为（c+2

2

，c），将点P₃（c+2

2

，c）代入y=

1

x

，可得c=

3

-

2

，
故点P₃的坐标为（

3

+

2

，

3

-

2

），
综上可得：P₁的坐标为（1，1），P₂的坐标为（

2

+1，

2

-1），P₃的坐标为（

3

+

2

，

3

-

2

），
总结规律可得：P_n坐标为：（

n

+

n-1

，

n

-

n-1

）．
则点P₂₀₁₄的坐标是（

2014

+

2013

，

2014

-

2013

）．
故答案是：（

2014

+

2013

，

2014

-

2013

）．

点评：本题考查了反比例函数的综合，涉及了点的坐标的规律变化，解答本题的关键是根据等腰三角形的性质结合反比例函数解析式求出P₁，P₂，P₃的坐标，从而总结出一般规律，难度较大．