题目内容
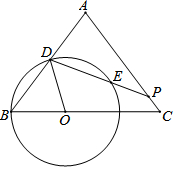
14. 如图,AB是⊙O的直径,C,D是⊙O上的点,且OC∥BD,AD分别与BC,OC相交于点E,F,则下列结论:①AD⊥BD;②∠AOC=∠AEC;③CB平分∠ABD;④AF=DF;⑤BD=2OF;⑥△CEF≌△BED,其中一定成立的①③④⑤(把你认为正确结论的序号都填上)
如图,AB是⊙O的直径,C,D是⊙O上的点,且OC∥BD,AD分别与BC,OC相交于点E,F,则下列结论:①AD⊥BD;②∠AOC=∠AEC;③CB平分∠ABD;④AF=DF;⑤BD=2OF;⑥△CEF≌△BED,其中一定成立的①③④⑤(把你认为正确结论的序号都填上)
分析 ①由直径所对圆周角是直角,
②由于∠AOC是⊙O的圆心角,∠AEC是⊙O的圆内部的角,
③由平行线得到∠OCB=∠DBC,再由同圆的半径相等得到结论判断出∠OBC=∠DBC;
④用半径垂直于不是直径的弦,必平分弦;
⑤用三角形的中位线得到结论;
⑥得不到△CEF和△BED中对应相等的边,所以不一定全等.
解答 解:①∵AB是⊙O的直径,
∴∠ADB=90°,
∴AD⊥BD,
故①正确;
②∵∠AOC是⊙O的圆心角,∠AEC是⊙O的圆内部的角,
∴∠AOC≠∠AEC,
故②不正确;
③∵OC∥BD,
∴∠OCB=∠DBC,
∵OC=OB,
∴∠OCB=∠OBC,
∴∠OBC=∠DBC,
∴BC平分∠ABD,
故③正确;
④∵AB是⊙O的直径,
∴∠ADB=90°,
∴AD⊥BD,
∵OC∥BD,
∴∠AFO=90°,
∵点O为圆心,
∴AF=DF,
故④正确;
⑤由④有,AF=DF,
∵点O为AB中点,
∴OF是△ABD的中位线,
∴BD=2OF,
故⑤正确;
⑥∵△CEF和△BED中,没有相等的边,
∴△CEF与△BED不全等,
故⑥不正确;
综上可知:其中一定成立的有①③④⑤,
故答案为:①③④⑤.
点评 本题主要考查圆周角定理及圆的有关性质、平行线的性质,掌握圆中有关的线段、角相等的定理是解题的关键,特别注意垂径定理的应用.

练习册系列答案
相关题目
19.数字970000用科学记数法表示为( )
| A. | 97×105 | B. | 9.7×105 | C. | 9.7×104 | D. | 0.97×104 |
6.若(x-2016)x=1,则x的值是( )
| A. | 2017 | B. | 2015 | C. | 0 | D. | 2017或0 |
3.计算正确的是( )
| A. | (-5)0=0 | B. | x3+x4=x7 | C. | (-a2b3)2=-a4b6 | D. | 2a2•a-1=2a |
4.已知直线y=(m-3)x-3m+1不经过第一象限,则m的取值范围是( )
| A. | m≥$\frac{1}{3}$ | B. | m≤$\frac{1}{3}$ | C. | $\frac{1}{3}$≤m<3 | D. | $\frac{1}{3}$≤m≤3 |
 如图,已知△ABC中,AB=AC=5,BC=6,点O是边BC上的动点,以点O为圆心,OB为半径作圆O,交AB边于点D,过点D作∠ODP=∠B,交边AC于点P,交圆O与点E.设OB=x.
如图,已知△ABC中,AB=AC=5,BC=6,点O是边BC上的动点,以点O为圆心,OB为半径作圆O,交AB边于点D,过点D作∠ODP=∠B,交边AC于点P,交圆O与点E.设OB=x. 请你根据学函数这一章所获得的学习经验来探究.
请你根据学函数这一章所获得的学习经验来探究.