题目内容
17.(1)化简:$\frac{2a}{{a}^{2}-9}-\frac{1}{a-3}$.(2)利用(1)中的结果解分式方程:$\frac{2x}{{x}^{2}-9}-\frac{1}{x-3}=\frac{1}{6}$.
分析 (1)原式通分并利用同分母分式的减法法则计算,约分即可得到结果;
(2)根据(1)的结果化简所求方程,求出解即可.
解答 解:(1)原式=$\frac{2a-(a+3)}{(a+3)(a-3)}$=$\frac{a-3}{(a+3)(a-3)}$=$\frac{1}{a+3}$;
(2)根据(1)化简分式方程得:$\frac{1}{x+3}$=$\frac{1}{6}$,
去分母得:x+3=6,
解得:x=3,
经检验x=3是增根,分式方程无解.
点评 此题考查了解分式方程,解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.解分式方程一定注意要验根.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
8.为了解甲、乙两种车的刹车距离,经试验发现,甲车的刹车距离s甲是车速v的$\frac{1}{5}$,乙车的刹车距离s乙等于反应距离与制动距离之和,二反应距离与车速v成正比,制动距离与车速v2成正比,具体关系如下表:
(1)分别求出s甲、s乙与车速v的函数关系式;
(2)若乙车在限速120km/h的高速公路上行驶,乙车的最长刹车距离是多少m?
(3)刹车速度是处理交通事故的一个重要因素,请看下面一个交通事故案例:甲、乙两车在限速为80km/g的道路上相向而行,等望见对方,同时刹车时已晚,两车还是相撞了,事后经现场勘查,测得甲车的刹车距离超过16m,但小于18m,乙车的刹车距离是24m,请你比较两车的速度,并判断哪辆车超速?
| 车速v(km/h) | 40 | 50 |
| 刹车距离s乙(m) | 12 | 17.5 |
(2)若乙车在限速120km/h的高速公路上行驶,乙车的最长刹车距离是多少m?
(3)刹车速度是处理交通事故的一个重要因素,请看下面一个交通事故案例:甲、乙两车在限速为80km/g的道路上相向而行,等望见对方,同时刹车时已晚,两车还是相撞了,事后经现场勘查,测得甲车的刹车距离超过16m,但小于18m,乙车的刹车距离是24m,请你比较两车的速度,并判断哪辆车超速?
5.若关于x的二次多项式5x2+mx-6可分解成两个一次式的乘积,则常数m不可能是( )
| A. | 17 | B. | 13 | C. | 7 | D. | -13 |
 已知,如图,?ABCD中,CN=AM,AE=CF,求证:EN∥MF.
已知,如图,?ABCD中,CN=AM,AE=CF,求证:EN∥MF.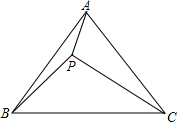 如图所示,设点P为△ABC内一点,∠PBA=10°,∠PCB=30°,∠BAP=20°,∠CBP=40°,求证:△ABC是等腰三角形.
如图所示,设点P为△ABC内一点,∠PBA=10°,∠PCB=30°,∠BAP=20°,∠CBP=40°,求证:△ABC是等腰三角形.