题目内容
5. 如图,两张宽度相等的纸条叠放在一起,重叠部分构成四边形ABCD.
如图,两张宽度相等的纸条叠放在一起,重叠部分构成四边形ABCD.(1)求证:四边形ABCD是菱形;
(2)若纸条宽3cm,∠ABC=60°,求四边形ABCD的面积.
分析 (1)首先可判断重叠部分为平行四边形,且两条纸条宽度相同;再由平行四边形的面积可得邻边相等,则重叠部分为菱形.
(2)解直角三角形求得菱形的边长,根据平行四边形的面积公式求得即可.
解答 解:(1)过点A作AE⊥BC于E,AF⊥CD于F,
∵两条纸条宽度相同,
∴AE=AF.
∵AB∥CD,AD∥BC,
∴四边形ABCD是平行四边形.
∵S?ABCD=BC•AE=CD•AF.
又∵AE=AF.
∴BC=CD,
∴四边形ABCD是菱形;
(2)在Rt△AEB中,∠AEB=90°,∠ABC=60°,AE=3cm,
∴AB=$\frac{AE}{sin60°}$=2$\sqrt{3}$cm,
∴BC=2$\sqrt{3}$cm,
∴四边形ABCD的面积=AE•BC=6$\sqrt{3}$cm2.
点评 本题考查了菱形的判定、解直角三角形以及四边形的面积,证得四边形为菱形是解题的关键..

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.2sin60°的值等于( )
| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $\sqrt{3}$ | C. | $\frac{{\sqrt{3}}}{4}$ | D. | $2\sqrt{3}$ |
20.下列立体图形中,俯视图是正方形的是( )
| A. |  | B. |  | C. |  | D. |  |
9.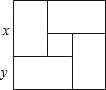 用四个全等的矩形和一个小正方形拼成如图所示的大正方形.已知大正方形的面积是196,小正方形的面积是4,若用x,y表示矩形的长和宽(x>y),则下列关系式中不正确的是( )
用四个全等的矩形和一个小正方形拼成如图所示的大正方形.已知大正方形的面积是196,小正方形的面积是4,若用x,y表示矩形的长和宽(x>y),则下列关系式中不正确的是( )
 用四个全等的矩形和一个小正方形拼成如图所示的大正方形.已知大正方形的面积是196,小正方形的面积是4,若用x,y表示矩形的长和宽(x>y),则下列关系式中不正确的是( )
用四个全等的矩形和一个小正方形拼成如图所示的大正方形.已知大正方形的面积是196,小正方形的面积是4,若用x,y表示矩形的长和宽(x>y),则下列关系式中不正确的是( )| A. | x+y=14 | B. | x-y=2 | C. | xy=48 | D. | x2+y2=144 |
10.若不等式组$\left\{\begin{array}{l}x-m<0\\ 1-2x≤7\end{array}\right.$有三个非负整数解,则m的取值范围是( )
| A. | 3<m<4 | B. | 2<m<3 | C. | 3<m≤4 | D. | 2<m≤3 |
 如图,⊙A的圆心A在反比例函数y=$\frac{3}{x}$(x>0)的图象上,且与x轴、y轴相切于点B、C,一次函数y=$\frac{{\sqrt{3}}}{3}$x+b的图象经过点C,且与x轴交于点D,与⊙A的另一个交点为点E.
如图,⊙A的圆心A在反比例函数y=$\frac{3}{x}$(x>0)的图象上,且与x轴、y轴相切于点B、C,一次函数y=$\frac{{\sqrt{3}}}{3}$x+b的图象经过点C,且与x轴交于点D,与⊙A的另一个交点为点E.